(本小题满分12分)
已知F1、F2分别是双曲线x2-y2=1的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线l:y=kx+b (b>0)与圆O相切,并与双曲线相交于A、B两点.
(1)根据条件求出b和k满足的关系式;
(2)向量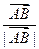 在向量
在向量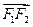 方向的投影是p,当(×)p2=1时,求直线l的方程;
方向的投影是p,当(×)p2=1时,求直线l的方程;
(3)当(× )p2=m且满足2≤m≤4时,求DAOB面积的取值范围.
)p2=m且满足2≤m≤4时,求DAOB面积的取值范围.
(本小题满分14分)对于定义在区间D上的函数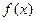 ,若存在闭区间
,若存在闭区间 和常数
和常数 ,使得对任意
,使得对任意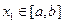 ,都有
,都有 ,且对任意
,且对任意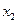 ∈D,当
∈D,当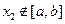 时,
时, 恒成立,则称函数
恒成立,则称函数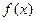 为区间D上的“平底型”函数.
为区间D上的“平底型”函数.
(Ⅰ)判断函数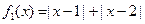 和
和 是否为R上的“平底
是否为R上的“平底 型”函数?并说明理由;
型”函数?并说明理由;
(Ⅱ)设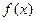 是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式
是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式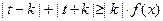 对一切
对一切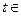 R恒成立,求实数
R恒成立,求实数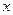 的取值范围;
的取值范围;
(Ⅲ)若函数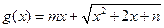 是区间
是区间 上的“平底型”函数,求
上的“平底型”函数,求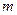 和
和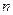 的值.
的值.
.
(本小题满分14分)已知椭圆 :
: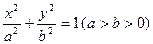 的离心率为
的离心率为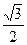 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线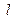 与
与 相交于
相交于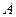 、
、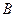 ,
, .
.
⑴求 、
、 的值;
的值;
⑵若动圆 与椭圆
与椭圆 和直线
和直线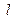 都没有公共点,试求
都没有公共点,试求 的取值范围.
的取值范围.
(本小题满分14分)
已知数列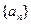 中,
中,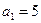 且
且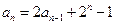 (
(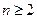 且
且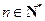 ).
).
(1)证明:数列 为
为 等差数列;
等差数列;
(2)求数列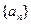 的前
的前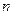 项和
项和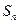 .
.
如图所示的长方体 中,底面
中,底面 是边长为
是边长为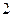 的正方形,
的正方形, 为
为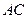 与
与 的交点,
的交点,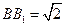 ,
,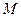 是线段
是线段 的中点.
的中点.
(Ⅰ)求证: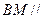 平面
平面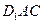 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角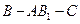 的大小.
的大小.
(本小题满分12分)
某校从参加某次“广州亚运”知识竞赛测试的学生中随机抽出 名学生,将其成绩(百分制)(均为整数)分成六段
名学生,将其成绩(百分制)(均为整数)分成六段 ,
, …
…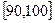 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求分数在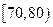 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的
平均分;
(Ⅲ)若从 名学生中
名学生中 随机抽取
随机抽取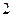 人,抽到的学生成绩在
人,抽到的学生成绩在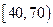 记
记 分,在
分,在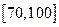 记
记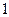 分,用
分,用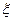 表示抽取结束后的总记分,求
表示抽取结束后的总记分,求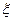 的分布列和数学期望.
的分布列和数学期望.