如图,四棱锥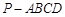 的底面是直角梯形,
的底面是直角梯形, ,
, ,
,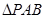 和
和 是两个边长为
是两个边长为 的正三角形,
的正三角形,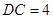 ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点.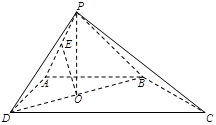
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面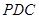 ;
;
(Ⅲ)求直线 与平面
与平面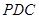 所成角的正弦值.
所成角的正弦值.
已知定义在区间(0,+∞)上的函数f(x)满足f =f(x1)-f(x2),且当x>1时,f(x)<0.
=f(x1)-f(x2),且当x>1时,f(x)<0.
(1)求f(1)的值;
(2)判断f(x)的单调性;
(3)若f(3)=-1,求f(x)在[2,9]上的最小值.
已知f(x)=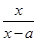 (x≠a).
(x≠a).
(1)若a=-2,试证明f(x)在(-∞,-2)内单调递增;
(2)若a>0且f(x)在(1,+∞)内单调递减,求a的取值范围.
规定[t]为不超过t的最大整数,例如[12.6]=12,[-3.5]=-4,对任意实数x,令f1(x)=[4x],g(x)=4x-[4x],进一步令f2(x)=f1[g(x)].
(1)若x=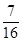 ,分别求f1(x)和f2(x);
,分别求f1(x)和f2(x);
(2)若f1(x)=1,f2(x)=3同时满足,求x的取值范围.
已知c>0,设命题p:函数y=cx为减函数.命题q:当x∈ 时,函数f(x)=x+
时,函数f(x)=x+ >
> 恒成立.如果p或q为真命题,p且q为假命题,求c的取值范围.
恒成立.如果p或q为真命题,p且q为假命题,求c的取值范围.
命题p:∀x∈(1,+∞),函数f(x)=|log2x|的值域为[0,+∞);命题q:∃m≥0,使得y=sin mx的周期小于 ,试判断p∨q,p∧q,
,试判断p∨q,p∧q, p的真假性.
p的真假性.