(本小题满分12分)
如图 ,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD =90o,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC的中点,AO交BD于E.
,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD =90o,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC的中点,AO交BD于E.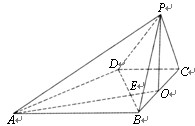
(1)求证:PA⊥BD;
(2)求二面角P—DC—B的 大小;
大小;
(本小题满分12分)
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,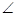 BCD=60
BCD=60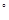 ,E是CD的中点,PA
,E是CD的中点,PA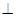 底面ABCD,PA=2.
底面ABCD,PA=2.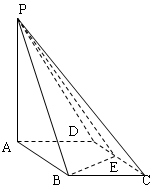
(1)证明:平面PBE 平面PAB;
平面PAB;
(2)求PC与平面PAB所成角的余弦值。
(本小题满分12分)
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是: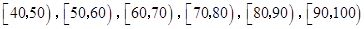 .
.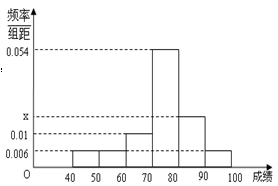
(1)求图中x的值;
(2)从成绩不低于80分的学生中按分层抽样抽取4人,选其中2人为数学课代表,求这两个人的数学成绩不在同一分数段的概率。
(本小题满分12分)在数列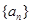 中,
中,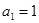 ,并且对于任意n∈N*,都有
,并且对于任意n∈N*,都有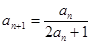 .
.
(1)证明数列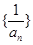 为等差数列,并求
为等差数列,并求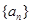 的通项公式;
的通项公式;
(2)设数列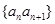 的前n项和为
的前n项和为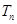 ,求使得
,求使得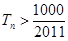 的最小正整数
的最小正整数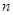 .
.
(本小题满分13分)
已知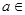 R,函数
R,函数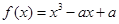 .
.
(1)求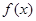 的单调区间;
的单调区间;
(2)证明:当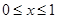 时,
时,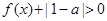 .
.
(本小题满分13分)
如图,已知椭圆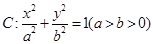 的焦点为
的焦点为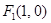 、
、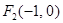 ,离心率为
,离心率为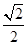 ,过点
,过点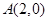 的直线
的直线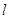 交椭圆
交椭圆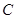 于
于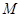 、
、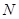 两点.
两点.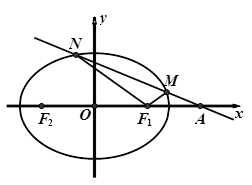
(1)求椭圆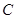 的方程;
的方程;
(2)①求直线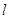 的斜率
的斜率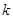 的取值范围;
的取值范围;
②在直线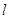 的斜率
的斜率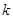 不断变化过程中,探究
不断变化过程中,探究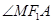 和
和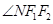 是否总相等?若相等,请给出证明,若不相等,说明理由.
是否总相等?若相等,请给出证明,若不相等,说明理由.