已知椭圆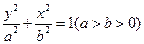 的离心率为
的离心率为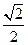 ,且两个焦点和短轴的一个端点是一个等腰三角形的顶点.斜率为
,且两个焦点和短轴的一个端点是一个等腰三角形的顶点.斜率为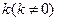 的直线
的直线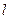 过椭圆的上焦点且与椭圆相交于
过椭圆的上焦点且与椭圆相交于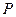 ,
, 两点,线段
两点,线段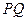 的垂直平分线与
的垂直平分线与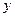 轴相交于点
轴相交于点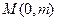 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)求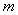 的取值范围;
的取值范围;
(Ⅲ)试用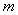 表示△
表示△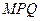 的面积,并求面积的最大值.
的面积,并求面积的最大值.
(本小题满分12分)已知圆C: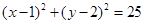 ,直线L:
,直线L: 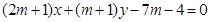
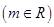
(1) 证明:无论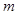 取什么实数,L与圆恒交于两点;
取什么实数,L与圆恒交于两点;
(2) 求直线被圆C截得的弦长最小时直线L的斜截式方程.
(本小题满分12分)如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.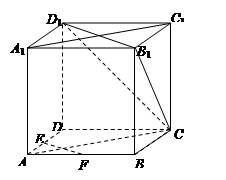
(1)求证:EF ∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1.
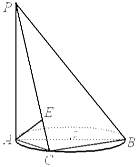
(本小题满分12分)如图,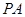 垂直于⊙
垂直于⊙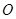 所在的平面,
所在的平面,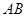 是⊙
是⊙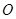 的直径,
的直径,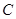 是⊙
是⊙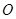 上一点,过点
上一点,过点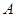 作
作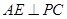 ,垂足为
,垂足为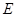 .
.
求证: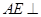 平面
平面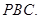
(本小题满分10分)过点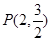 的直线
的直线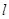 与
与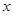 轴的正半轴、
轴的正半轴、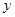 轴的正半轴分别交于点
轴的正半轴分别交于点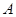 、
、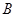 ,
,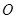 为坐标原点,
为坐标原点,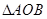 的面积等于6,求直线
的面积等于6,求直线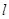 的方程.
的方程.
(本题满分12分)已知函数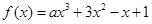 在R上是减函数,求实数
在R上是减函数,求实数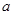 的取值范围。
的取值范围。