(本题12分)
某家具城进行促销活动,促销方案是:顾客每消费1000元,便可以获得奖券一张,每张奖券中奖的概率为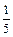 ,若中奖,则家具城返还顾客现金200元. 某顾客购买一张价格为3400元的餐桌,得到3张奖券.
,若中奖,则家具城返还顾客现金200元. 某顾客购买一张价格为3400元的餐桌,得到3张奖券.
(I)求家具城恰好返还该顾客现金200元的概率;
(II)求家具城至少返还该顾客现金200元的概率.
(本小题满分8分)已知平面向量a ,b
,b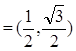
(Ⅰ)若存在实数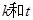 ,满足x
,满足x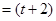 a
a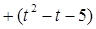 b,y
b,y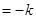 a
a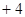 b且x⊥y,求出
b且x⊥y,求出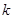 关于
关于 的关系式
的关系式 ;
;
(Ⅱ)根据(Ⅰ)的结论,试求出函数 在
在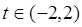 上的最小值.
上的最小值.
(本小题满分8分)设函数 的图象在
的图象在 处的切线方程为
处的切线方程为 .
.
(Ⅰ)求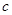 ,
,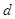 ;
;
(Ⅱ)若函数在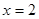 处取得极值
处取得极值 ,试求函数解析式并确定函数的单调区间.
,试求函数解析式并确定函数的单调区间.
(本小题满分8分)
已知 是一个公差大于0的等差数列,且满足
是一个公差大于0的等差数列,且满足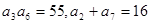 .
.
(Ⅰ)求数列 的通项公式:
的通项公式:
(Ⅱ)等比数列 满足:
满足: ,若数列
,若数列 ,求数列
,求数列 的前n项和
的前n项和 .
.
(本小题满分8分)在 中,
中, 分别为内角
分别为内角 的对边,且
的对边,且
(Ⅰ)求 的大小;
的大小;
(Ⅱ)若 ,试求内角B、C的大小.
,试求内角B、C的大小.
(本小题满分8分)设函数 的定义域为
的定义域为 .
.
(Ⅰ)若 ,
, ,求实数
,求实数 的范围;
的范围;
(Ⅱ)若函数
 的定义域为
的定义域为 ,求实数
,求实数 的取值范围.
的取值范围.