已知曲线C1的参数方程为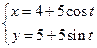 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为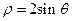 .
.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).
已知(1+x+mx2)10的展开式中x4的系数大于-330,求m的取值范围.
20个相同的小球,全部装入编号为1,2,3的三个盒子里,每个盒子内所放的球数不小于盒子的编号数,求共有多少种不同的放法?
已知10件不同产品中共有4件次品,现对它们进行一一测试,直至找到所有次品为止.
(1)若恰在第5次测试,才测试到第一件次品,第10次才找到最后一件次品的不同测试方法数有多少种?
(2)若恰在第5次测试后,就找出了所有次品,则这样的不同测试方法数有多少种?
某城市在中心广场建造一个花圃,花圃分为6个部分(如图).现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有多少种(用数字作答).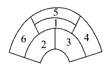
某体育彩票规定:从01到36共36个号中抽出7个号为一注,每注2元.某人想先选定吉利号18,然后从01至17中选3个连续的号,从19至29中选2个连续的号,从30至36中选1个号组成一注.若这个人要把这种要求的号全买下,则至少要花多少元钱?