..(本小题满分12分)
数列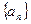 的各项均为正数,
的各项均为正数,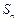 为其前
为其前 项和,对于任意
项和,对于任意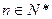 ,总有
,总有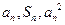 成等差数列.
成等差数列.
(1)求数列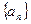 的通项公式;
的通项公式;
(2)设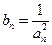 ,数列
,数列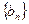 的前
的前 项和为
项和为 ,求证:
,求证: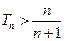 .
.
(本小题满分14分)
广州市为了做好新一轮文明城市创建工作,有关部门为了解市民对《广州市创建全国文明城市小知识》的熟知程度,对下面两个问题进行了调查:
问题一:《广州市民“十不”行为规范》有哪“十不”?
问题二:广州市“一约三则”的内容是什么?
调查结果显示, 年龄段的市民回答第一个问题的正确率为
年龄段的市民回答第一个问题的正确率为 ,
, 年龄段的市民回答第二个问题正确率为
年龄段的市民回答第二个问题正确率为 .
.
为使活动得到市民更好的配合,调查单位采取如下激励措施:正确回答问题一者奖励价值20元的礼物;正确回答问题二奖励价值30元的礼物,有一家庭的两成员(大人42岁,孩子13岁)参与了此项活动,小孩回答第一个问题,大人回答第二个问题,问这个家庭获得礼物价值的数学期望是多少?
(本小题满分14分)如图,已知四棱锥 的底面
的底面 是矩形,
是矩形, 、
、 分别是
分别是 、
、 的中点,
的中点, 底面
底面 ,
, ,
,
(1)求证: 平面
平面
(2)求二面角 的余弦值
的余弦值
(本小题满分14分)
观察下列三个三角恒等式
(1)
(2)
(3)
的特点,由此归纳出一个一般的等式,使得上述三式为它的一个特例,并证明你的结论
(说明:本题依据你得到的等式的深刻性分层评分.)
(本小题满分12分)
已知 的两个顶点
的两个顶点 的坐标为
的坐标为 ,且
,且 的斜率之积等于
的斜率之积等于 ,若顶点
,若顶点 的轨迹是双曲线(去掉两个顶点),求
的轨迹是双曲线(去掉两个顶点),求 的取值范围.
的取值范围.
(本小题满分12分)
已知函数
(1)求
(2)求函数 的单调区间
的单调区间