下列命题的说法错误的是( )
A.命题“若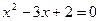 ,则 ,则 ”的逆否命题为:“若 ”的逆否命题为:“若 ,则 ,则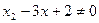 ”。 ”。 |
B.“ ”是“ ”是“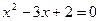 ”的充分不必要条件 ”的充分不必要条件 |
C.若 的假命题,则p、q均为假命题 的假命题,则p、q均为假命题 |
D.对于命题P: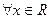 ,均有 ,均有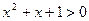 ,则﹁P: ,则﹁P: ,使得 ,使得 [来 [来 |
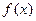 是定义在
是定义在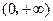 上的非负可导函数,且满足
上的非负可导函数,且满足 .对任意正数
.对任意正数 ,若
,若 ,则必有()
,则必有()
A.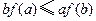 |
B.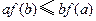 |
C.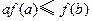 |
D. |
设 是至少含有两个元素的集合,在
是至少含有两个元素的集合,在 上定义了一个二元运算“*”(即对任意的
上定义了一个二元运算“*”(即对任意的 ,对于有序元素对(
,对于有序元素对( ),在
),在 中有唯一确定的元素
中有唯一确定的元素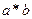 与之对应).若对任意的
与之对应).若对任意的 ,有
,有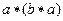
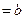 ,则对任意的
,则对任意的 ,下列等式中不恒成立的是()
,下列等式中不恒成立的是()
A. |
B. |
C.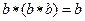 |
D. |
设 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且 满足:“当
满足:“当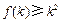 成立时,总可推出
成立时,总可推出
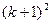 成立”。那么,下列命题总成立的是( )
成立”。那么,下列命题总成立的是( )
A.若 成立,则 成立,则 成立 成立 |
B.若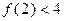 成立,则 成立,则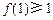 成立 成立 |
C.若 成立,则当 成立,则当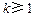 时,均有 时,均有 成立 成立 |
D.若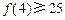 成立,则当 成立,则当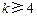 时,均有 时,均有 成立 成立 |
观察式子: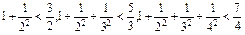 ,…,则可归纳出式子为()
,…,则可归纳出式子为()
A. |
B.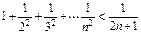 |
C. |
D.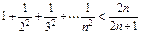 |
设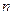 为正整数,
为正整数,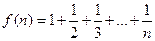 ,经计算得
,经计算得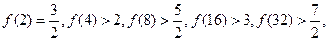 观察上述结果,可推测出一般结论( )
观察上述结果,可推测出一般结论( )
A.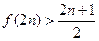 |
B.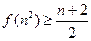 |
C.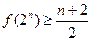 |
D.以上都不对 |