已知二次函数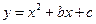 中,函数
中,函数 与自变量
与自变量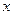 的部分对应值如下表:
的部分对应值如下表:
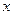 |
… |
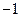 |
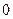 |
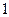 |
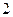 |
 |
 |
… |
 |
… |
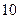 |
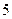 |
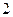 |
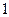 |
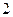 |
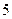 |
… |
(1)求该二次函数的关系式;( 2)当
2)当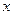 为何值时,
为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?
(3)若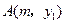 ,
,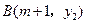 两点都在该函数的图象上,试比较
两点都在该函数的图象上,试比较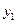 与
与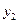 的大小.
的大小.
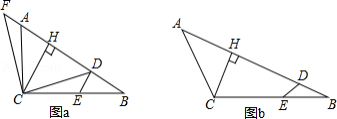
如图,在 中, ,点 在 上, ,点 在 上,连接 , ,作 ,垂足为 .
(1)如图 ,当 时,连接 ,过点 作 交 的延长线于点 .
①求证: ;
②请猜想三条线段 , , 之间的数量关系,直接写出结论;
(2)如图 ,当 时,三条线段 , , 之间存在怎样的数量关系?请证明你的结论.
有一家苗圃计划植桃树和柏树,根据市场调查与预测,种植桃树的利润 (万元)与投资成本 (万元)满足如图①所示的二次函数 ;种植柏树的利润 (万元)与投资成本 (万元)满足如图②所示的正比例函数 .
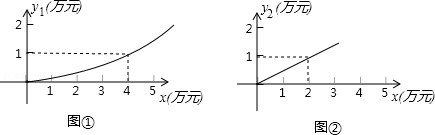
(1)分别求出利润 (万元)和利润 (万元)关于投资成本 (万元)的函数关系式;
(2)如果这家苗圃以10万元资金投入种植桃树和柏树,桃树的投资成本不低于2万元且不高于8万元,苗圃至少获得多少利润?最多能获得多少利润?
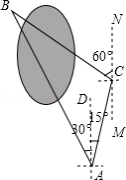
小明要测量公园被湖水隔开的两棵大树 和 之间的距离,他在 处测得大树 在 的北偏西 方向,他从 处出发向北偏东 方向走了200米到达 处,测得大树 在 的北偏西 方向.
(1)求 的度数;
(2)求两棵大树 和 之间的距离(结果精确到1米)(参考数据: , ,
如图, 是 的直径,点 是 上一点,连接 , ,作 ,垂足为 .
(1)求证: 是 的切线;
(2)若 , ,求图中阴影部分的面积.

某电视台为了解本地区电视节目的收视情况,对部分观众开展了“你最喜爱的电视节目”的问卷调查(每人只填写一项),根据收集的数据绘制了下面两幅不完整的统计图,根据要求回答下列问题:
(1)本次问卷调查共调查了 名观众;
(2)图②中最喜爱“新闻节目”的人数占调查总人数的百分比为 ,“综艺节目”在扇形统计图中所对应的圆心角的度数为 ;
(3)补全图①中的条形统计图;
(4)现有最喜爱“新闻节目”(记为 ,“体育节目”(记为 ,“综艺节目”(记为 ,“科普节目”(记为 的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“ ”和“ ”两位观众的概率.