如图，M、N、P分别是正方体ABCD－A1B1C1D1的棱AB、BC、DD1上的点．
(1)若＝，求证：无论点P在D1D上如何移动，总有BP⊥MN；
(2)若D1P：PD＝1∶2，且PB⊥平面B1MN，求二面角M－B1N－B的余弦值；
(3)棱DD1上是否总存在这样的点P，使得平面APC1⊥平面ACC1？证明你的结论．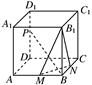
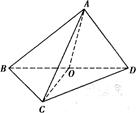
如图，在三棱锥A-BCD中，△ABD和△BCD是两个全等的等腰直角三角形，O为BD的中点，且AB=AD=CB=CD=2，AC=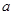
．
(1)当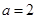
时，求证：AO⊥平面BCD；
(2)当二面角
的大小为
时，求二面角
的正切值．
已知函数
．
(1)求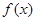
的最小正周期及其单调增区间：
(2)当
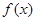时，求的值域．
已知函数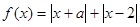
（1）当
的解集
（2）若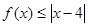
的解集包含[1，2]，求
的取值范围
已知函数
（1）求证：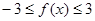 
（2）求不等式 
的解集
在雅安发生地震灾害之后，救灾指挥部决定建造一批简易房，供灾区群众临时居住，房形为长方体，高2.5米，前后墙用2.5米高的彩色钢板，两侧用2.5米高的复合钢板，两种钢板的价格都用长度来计算（即钢板的高均为2.5米，用长度乘以单价就是这块钢板的价格），每米单价：彩色钢板为450元，复合钢板为200元，房顶用其他材料建造，每平方米材料费为200元，每套房材料费控制在32000元以内。
（1）设房前面墙的长为
，两侧墙的长为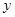
，一套简易房所用材料费为p，试用
。
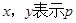（2）一套简易房面积S的最大值是多少？当S最大时，前面墙的长度是多少？