(本小题满分14分)
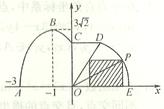
如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y= (A>0,
(A>0,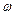 >0,
>0,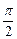 <
<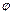 <
< ),x∈[-3,0]的图象,且图象的最高点为B(-1,
),x∈[-3,0]的图象,且图象的最高点为B(-1, );赛道的中间部分为
);赛道的中间部分为 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧 .
.
(1)求 ,
, 的值和∠DOE的值;
的值和∠DOE的值;
(2)若要在圆弧赛道所对应的扇形区域内建一个“矩形草坪”,如图所示,矩形的一边在道路AE上,一个顶点在扇形半径OD上.记∠POE= ,求当“矩形草坪”的面积最大时
,求当“矩形草坪”的面积最大时 的值.
的值.
已知向量a=(tanx,1),b=(sinx,cosx),其中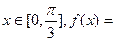 a·b.
a·b.
(I)求函数 的解析式及最大值;
的解析式及最大值;
(II)若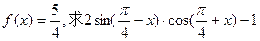 的值.
的值.
已知向量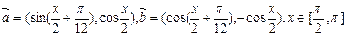 ,函数
,函数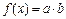 .
.
(I)若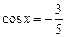 ,求函数
,求函数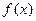 的值;
的值;
(II)将函数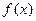 的图象按向量c=
的图象按向量c=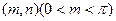 平移,使得平移后的图象关于原点对称,求向量c.
平移,使得平移后的图象关于原点对称,求向量c.
已知函数f(x)=2sinxcosx+cos2x.
(Ⅰ)求f (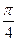 )的值;
)的值;
(Ⅱ)设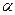 ∈(0,
∈(0,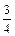
 ),f (
),f (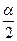 )=
)=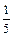 ,求cos2
,求cos2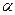 的值.
的值.
已知函数f(x)= ·
· ,其中
,其中 =(sinωx+cosωx,
=(sinωx+cosωx, cosωx),
cosωx), =cosωx-sinωx,2sinωx)(ω>0),若f(x)相邻的对称轴之间的距离不小于
=cosωx-sinωx,2sinωx)(ω>0),若f(x)相邻的对称轴之间的距离不小于 .
.
(1)求ω的取值范围;
(2)在△ABC中,a,b,c分别为A,B,C的对边,a= ,b+c=3,当ω最大时,f(A)=1,求△ABC的面积.
,b+c=3,当ω最大时,f(A)=1,求△ABC的面积.
在△ABC中,角A、B、C所对边分别为a,b,c,已知 ,且最长边的边长为l.求:
,且最长边的边长为l.求:
(I)角C的大小;
(II)△ABC最短边的长.