已知二次函数y=f1(x)的图象以原点为顶点且过点(1,1),反比例函数y=f2(x)的图象与直线y=x的两个交点间距离为8,f(x)=f1(x)+f2(x).
(1)求函数f(x)的表达式;
(2)证明:当a>3时,关于x的方程f(x)=f(a)有三个实数解
如图,在几何体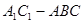 中,四边形
中,四边形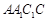 为平行四边形,且面
为平行四边形,且面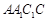
 面
面 ,
, ,且
,且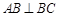 ,
,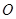 为
为 中点.
中点.
(Ⅰ)证明: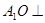 平面
平面 ;
;
(Ⅱ)求直线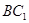 与平面
与平面 所成角的正弦值.
所成角的正弦值.
已知直线l平行于直线 ,直线l与两坐标轴围成的三角形周长是15,求直线l的方程.
,直线l与两坐标轴围成的三角形周长是15,求直线l的方程.
某几何体的三视图及其尺寸如右图,求该几何体的表面积和体积.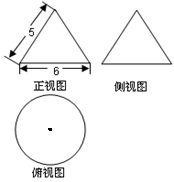
已知函数: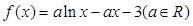
(I)讨论函数 的单调性;
的单调性;
(II)若函数 的图象在点
的图象在点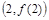 处的切线的倾斜角为45o,是否存在实数m使得对于任意的
处的切线的倾斜角为45o,是否存在实数m使得对于任意的 ,函数
,函数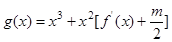 在区间
在区间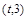 上总不是单调函数?若存在,求m的取值范围;否则,说明理由;
上总不是单调函数?若存在,求m的取值范围;否则,说明理由;
(Ⅲ)求证: .
.
已知函数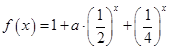 ;
;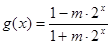 .
.
(I)当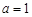 时,求函数f(x)在
时,求函数f(x)在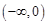 上的值域;
上的值域;
(II)若对任意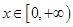 ,总有
,总有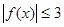 成立,求实数
成立,求实数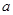 的取值范围;
的取值范围;
(Ⅲ)若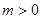 (
(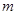 为常数),且对任意
为常数),且对任意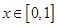 ,总有
,总有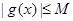 成立,求M的取值范围.
成立,求M的取值范围.