为了解学生的课余生活情况,某中学在全校范围内随机抽取部分学生进行问卷调查. 问卷中请学生选择最喜欢的课余生活种类(每人只选一类),选项有音乐类、美术类、体育类及其他共四类,调查后将数据绘制成扇形统计图和条形统计图(如图所示). 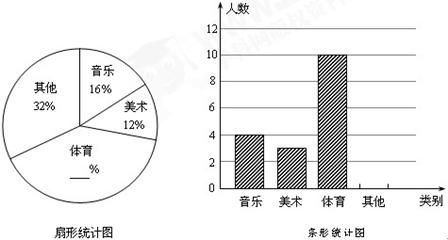
(1)请根据所给的扇形图和条形图,填写出扇形图中缺失的数据,并把条形图补充完整;
(2)在问卷调查中,小丁和小李分别选择了音乐类和美术类,校学生会要从选择音乐类和美术类的学生中分别抽取一名学生参加活动,用列表或画树状图的方法求小丁和小李恰好都被选中的概率 ;
;
(3)如果该学校有500名学生,请你估计该学校中最喜欢体育运动的学生约有多少名?
如图,有一圆柱油罐,已知油罐的底面圆的周长是12米,高是5米,要从点A起环绕油罐建梯子,梯子的顶端正好到达点A的正上方点B,则梯子最短需多长?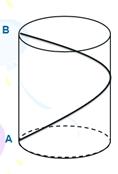
(1)
(2)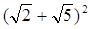
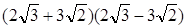
(4)
在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r.则称P′为点P关于⊙C的反称点,下图为点P及其关于⊙C的反称点P′的示意图.
特别地,当点P′与圆心C重合时,规定CP′=0.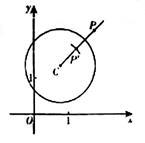
(1)当⊙O的半径为1时.
①分別判断点M(2,1),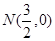 ,
,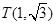 关于⊙O的反称点是否存在?若存在,求其坐标;
关于⊙O的反称点是否存在?若存在,求其坐标;
②点P在直线y=-x+2上,若点P关于⊙O的反称点P′存在,且点P′不在x袖上,求点P的横坐标的取值范围;
(2)⊙C的圆心在x袖上,半径为1,直线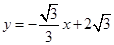 与x轴、y轴分別交于点A,B.若线段AB存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
与x轴、y轴分別交于点A,B.若线段AB存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
(.重庆市B卷,第26题,12分)如图,抛物线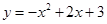 与x轴交与A,B两点(点A在点B的左侧),与y轴交于点C. 点D和点C关于抛物线的对称轴对称,直线AD与y轴相交于点E.
与x轴交与A,B两点(点A在点B的左侧),与y轴交于点C. 点D和点C关于抛物线的对称轴对称,直线AD与y轴相交于点E.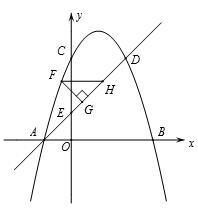
(1)求直线AD的解析式;
(2)如图,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH的周长的最大值;
(3)点M是抛物线的顶点,点P是y轴上一点,点Q是坐标平面内一点,以A,M,P,Q为顶点的四边形是AM为边的矩形,若点T和点Q关于AM所在直线对称,求点T的坐标.
(.重庆市A卷,第26题,12分)如图1,在平面直角坐标系中,抛物线 交
交 轴于A,B两点(点A在点B的左侧),交
轴于A,B两点(点A在点B的左侧),交 轴于点W,顶点为C,抛物线的对称轴与
轴于点W,顶点为C,抛物线的对称轴与 轴的交点为D。
轴的交点为D。
图1
(1)求直线BC的解析式;
(2)点E(m,0),F(m+2,0)为 轴上两点,其中
轴上两点,其中 ,
, ,
, 分别垂直于
分别垂直于 轴,交抛物线与点
轴,交抛物线与点 ,
, ,交BC于点M,N,当
,交BC于点M,N,当 的值最大时,在
的值最大时,在 轴上找一点R,使
轴上找一点R,使 的值最大,请求出R点的坐标及
的值最大,请求出R点的坐标及 的最大值;
的最大值;
(3)如图2,已知 轴上一点
轴上一点 ,现以P为顶点,
,现以P为顶点, 为边长在
为边长在 轴上方作等边三角形QPG,使GP⊥
轴上方作等边三角形QPG,使GP⊥ 轴,现将△QPG沿PA方向以每秒1个单位长度的速度平移,当点P到达点A时停止,记平移后的△QPG为
轴,现将△QPG沿PA方向以每秒1个单位长度的速度平移,当点P到达点A时停止,记平移后的△QPG为 ,设
,设 与△ADC的重叠部分面积为s,当点
与△ADC的重叠部分面积为s,当点 到
到 轴的距离与点
轴的距离与点 到直线AW的距离相等时,求s的值。
到直线AW的距离相等时,求s的值。
|
