如图,飞机沿水平方向(A、B两点所在直线)飞行,前方有一座高山,为了避免飞机飞行过低,就必须测量山顶M到飞行路线AB的距离MN.飞机能够测量的数据有俯角和飞行的距离(因安全因素,飞机不能飞到山顶的正上方N处才测飞行距离),请设计一个距离MN的方案,要求:
(1)指出需要测量的数据(用字母表示,并在图中标出);
(2)用测出的数据写出求距离MN的步骤.
 |
如图所示,某校一块长为2a米的正方形空地是七年级4个班的清洁区,其中分给七(1)班的清洁区是一块边长为 米的正方形,
米的正方形, 。
。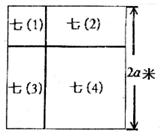
(1)分别求出七(2)、七(3)班的清洁区的面积;
(2)七(4)班的清洁区的面积比七(1)班的清洁区的面积多多少平方米?
已知∠1=∠2=∠3=59°,求∠4的度数。
先化简,再求值: ,其中
,其中
计算
(1)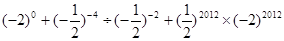
(2)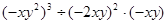
如图①,正方形 ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形 ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以相同速度在x轴正半轴上运动,当P点到达D点时,两点同时停止运动,设运动的时间为t秒.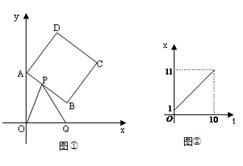
(1)当P点在边AB上运动时,点Q的横坐标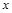 (长度单位)关于运动时间t(秒)的函数图象如图②所示,请直接写出点Q开始运动时的坐标及点P运动速度;
(长度单位)关于运动时间t(秒)的函数图象如图②所示,请直接写出点Q开始运动时的坐标及点P运动速度;
(2)求正方形边长及顶点C的坐标;
(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标;
(4)如果点P、Q保持原速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等,若能,直接写出所有符合条件的t的值;若不能,请说明理由.