在边长为1的正方形网格中,正方形 与正方形
与正方形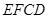 的位置如图所示.
的位置如图所示.
(1)请你按下列要求画图:
① 联结 交
交 于点
于点 ;
;
② 在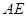 上取一点
上取一点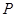 ,联结
,联结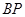 ,
,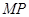 ,使△
,使△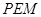 与△
与△ 相似;
相似;
(2)若 是线段
是线段 上一点,连结
上一点,连结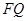 并延长交四边形
并延长交四边形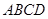 的一边于点
的一边于点 ,且满足
,且满足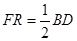 ,则
,则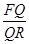 的值为_____________.
的值为_____________.
(本题9分)喝绿茶前需要烧水和泡茶两个工序,即需要将电热水壶中的水烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温y(℃)与时间x(min)成一次函数关系;停止加热过了1分钟后,水壶中水的温度 y(℃)与时间x(min)近似于反比例函数关系(如图).已知水壶中水的初始温度是20℃,降温过程中水温不低于20℃.
(1)分别求出图中所对应的函数关系式,并且写出自变量x的取值范围;
(2)从水壶中的水烧开(100℃)降到80℃就可以进行泡制绿茶,问从水烧开到泡茶需要等待多长时间?
(本题8分)设点A的坐标(x,y),其中横坐标x可取-1,2,纵坐标y可取-1,1,2。
(1)求出点A的坐标的所有等可能结果(用树形图或列表法求解);
(2)求点A与点B(1,-1)关于原点对称的概率。
(本题5分)为了构建城市立体道路网络,决定修建一条轻轨铁路,为了使工程提前6个月完成,需将原定的工作效率提高25%.原计划完成这项工程需要多少个月?
(本题5分)如图所示,已知BD⊥CD于D,EF⊥CD于F, ,
,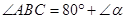 ,其中
,其中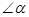 为锐角,求证:
为锐角,求证: 。
。
(本题7分)如图,已知A (4,a),B (﹣2,﹣4)是一次函数y=kx+b的图象和反比例函数y=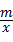 的图象的交点.
的图象的交点.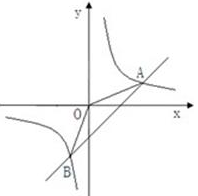
(1)求反比例函数和一次函数的解祈式;
(2)求△A0B的面积.