(本小题满分15分)
设函数 ,其中,
,其中,
(1)求函数 的极值和单调区间;;w
的极值和单调区间;;w
(2)已知函数 有3个不同的零点
有3个不同的零点 ,且
,且 ,若对任意的
,若对任意的 ,
, 恒成立,求
恒成立,求 的取值范围
的取值范围
已知 为等差数列,其前
为等差数列,其前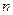 项和为
项和为 ,
,
若 ……
……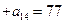 ,且
,且
(Ⅰ)求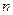 值;(Ⅱ)若
值;(Ⅱ)若 ,求
,求 的值
的值
求与直线
 平行且距离等于
平行且距离等于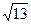 的直线
的直线 方程.
方程.
(本小题满分14分)
如图,在长方体ABCD─A1B1C1D1中,E、P分别是BC、A1D1的中点,M、N分别是AE、CD1的中点,AD=AA1=a,AB=2a.
(1)求证:MN∥面ADD1A1;
(2)求二面角P─AE─D的大小;
(3)求三棱锥P─DEN的体积.
.如图:正三棱柱ABC—A1B1C1中,D是BC的中点,AA1=AB=1.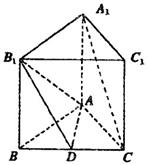
(1)求证:A1C//平面AB1D;
(2)求二面角B—AB1—D的大小;
( 3)求点C到平面AB1D的距离.
3)求点C到平面AB1D的距离.
将两块三 角板按图甲方式拼好,其中
角板按图甲方式拼好,其中 ,
, ,
, ,AC = 2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙.
,AC = 2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙.
(I)求证:BC ⊥AD;
(II)求证 :O为线段AB中点;
:O为线段AB中点;
(III)求二面角D-AC-B的大小的正弦值.