放射性同位素C被考古学家称为“碳钟”,它可以用来判定古生物体的年代,此项研究获得1960年诺贝尔化学奖.
(1)宇宙射线中高能量的中子碰到空气中的氮原子后,会形成很不稳定的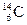 ,它很容易发生衰变,放出β射线变成一个新核,其半衰期为5 730年.试写出此核反应方程.
,它很容易发生衰变,放出β射线变成一个新核,其半衰期为5 730年.试写出此核反应方程.
(2)若测得一古生物遗骸中的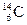 含量只有活体中的25%,则此遗骸距今约有多少年?[
含量只有活体中的25%,则此遗骸距今约有多少年?[
如图所示,倾角为37°的光滑绝缘的斜面上放着M=1kg的U型导轨abcd,ab∥cd。另有一质量m=1kg的金属棒EF平行bc放在导轨上,EF下侧有绝缘的垂直于斜面的立柱P、S、Q挡住EF使之不下滑。以OO′为界,下部有一垂直于斜面向下的匀强磁场,上部有平行于斜面向下的匀强磁场。两磁场的磁感应强度均为B=1T,导轨bc段长L=1m。金属棒EF的电阻R=1.2Ω,其余电阻不计。金属棒与导轨间的动摩擦因数μ=0.4,开始时导轨bc边用细线系在立柱S上,导轨和斜面足够长。当剪断细线后,试求: 
(1)细线剪短瞬间,导轨abcd运动的加速度;
(2)导轨abcd运动的最大速度;
(3)若导轨从开始运动到最大速度的过程中,流过金属棒EF的电量q=5C,则在此过程中,系统损失的机械能是多少?(sin37°=0.6)
如图所示,某传送带装置倾斜放置,倾角 =37o,传送带AB长度xo=l0m。有一水平平台CD高度保持6.45m不变。现调整D端位置,当D、B的水平距离合适时,自D端水平抛出的物体恰好从B点沿BA方向冲上斜面,此后D端固定不动,g=l0m/s2。另外,传送带B端上方安装一极短的小平面,与传送带AB平行共面,保证自下而上传送的物体能沿AB方向由B点斜向上抛出。(sin37o=0.6,cos37o=0.8)
=37o,传送带AB长度xo=l0m。有一水平平台CD高度保持6.45m不变。现调整D端位置,当D、B的水平距离合适时,自D端水平抛出的物体恰好从B点沿BA方向冲上斜面,此后D端固定不动,g=l0m/s2。另外,传送带B端上方安装一极短的小平面,与传送带AB平行共面,保证自下而上传送的物体能沿AB方向由B点斜向上抛出。(sin37o=0.6,cos37o=0.8)
(1)求D、B的水平距离;
(2)若传送带以5m/s的速度逆时针匀速运行,某物体甲与传送带间动摩擦因数 1=0.9,自A点沿传送带方向以某一初速度冲上传送带时,恰能水平落到水平台的D端,求物体甲的最大初速度vo1
1=0.9,自A点沿传送带方向以某一初速度冲上传送带时,恰能水平落到水平台的D端,求物体甲的最大初速度vo1
(3)若传送带逆时针匀速运行,某物体乙与传送带间动摩擦因数 2=0.6,自A点以vo2=11m/s的初速度沿传送带方向冲上传送带时,恰能水平落到水平台的D端,求传送带的速度v′。
2=0.6,自A点以vo2=11m/s的初速度沿传送带方向冲上传送带时,恰能水平落到水平台的D端,求传送带的速度v′。
如图a所示,竖直光滑杆固定不动,上面套有下端接触地面的轻弹簧和一个小物体。将小物体在一定高度静止释放,通过传感器测量到小物体的速度和离地高度h并做出其动能-高度图b。其中高度从0.35m下降到0.3m范围内图像为直线,其余部分为曲线。以地面为零势能面,根据图像求:
(1)小物体的质量m为多少?
(2)轻弹簧弹性势能最大时,小物体的动能与重力势能之和为多大?
(3)把小物体和轻弹簧作为一个系统研究,系统具有的最小势能为多少?
如图所示,两个截面积都为S的圆柱形容器,右边容器高为H,上端封闭,左边容器上端是一个可以在容器内无摩擦滑动的质量为M的活塞。两容器由装有阀门的极细管道相连,容器、活塞和细管都是绝热的。开始时阀门关闭,左边容器中装有理想气体,平衡时活塞到容器底的距离为H,右边容器内为真空。现将阀门缓慢打开,活塞便缓慢下降,直至系统达到新的平衡,此时理想气体的温度增加为原来的1.4倍,已知外界大气压强为p0,求此过程中气体内能的增加量。
粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,且沿x轴方向的电势j与坐标值x的关系如下表格所示:
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
| x/m |
0.05 |
0.10 |
0.15 |
0.20 |
0.25 |
0.30 |
0.35 |
0.40 |
0.45 |
| φ/105v |
9.00 |
4.50 |
3.00 |
2.25 |
1.80 |
1.50 |
1.29 |
1.13 |
1.00 |
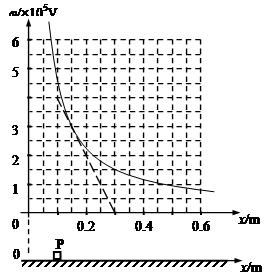
根据上述表格中的数据可作出如右的j—x图像。现有一质量为0.10kg,电荷量为1.0´10-7C带正电荷的滑块(可视作质点),其与水平面的动摩擦因素为0.20。问:
(1)由数据表格和图像给出的信息,写出沿x轴的电势j与x的函数关系表达式。
(2)若将滑块无初速地放在x=0.10m处,则滑块最终停止在何处?
(3)在上述第(2)问的整个运动过程中,它的加速度如何变化?当它位于x=0.15m时它的加速度多大?
(4)若滑块从x=0.60m处以初速度v0沿-x方向运动,要使滑块恰能回到出发点,其初速度v0应为多大?