在某学校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次.某同学在A处的命中率q1为0.25,在B处的命率为q2.该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮训练结束后所得的总分,其分布列为
| ξ |
0 |
2 |
3 |
4 |
5 |
| P |
0.03 |
P1 |
P2 |
P3 |
P4 |
(1)求q2的值;
(2)求随机变量ξ的数学期望Eξ;
(3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
对 ,记
,记 ,函数
,函数
(1)求 ,
, ;
;
(2)作出 的图像;
的图像;
(3)若关于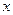 的方程
的方程 有且仅有两个不等的解,求实数
有且仅有两个不等的解,求实数 的取值范围.
的取值范围.

.已知 ,
,
(1)求证: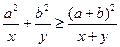 ,并指出等号成立的条件;
,并指出等号成立的条件;
(2)利用此不等式求函数 的最小值,并求出等号成立时的
的最小值,并求出等号成立时的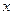 值.
值.
.解关于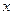 的不等式
的不等式 。
。
.围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。
(Ⅰ)将y表示为x的函数
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,求出最小总费用。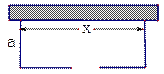
已知关于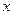 的不等式
的不等式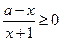 的解集为
的解集为 ,不等式
,不等式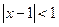 的解集为
的解集为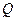
(1)若 ,求
,求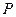 ;(2)若
;(2)若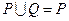 ,求正数
,求正数 的取值范围。
的取值范围。