已知构成某系统的元件能正常工作的概率为p(0<p<1),且各个元件能否正常工作是相互独立的.今有2n(n大于1)个元件可按下图所示的两种联结方式分别构成两个系统甲、乙.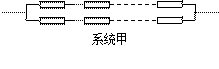
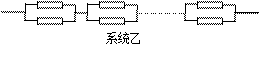
(1)试分别求出系统甲、乙能正常工作的概率p1,p2;
(2)比较p1与p2的大小,并从概率意义上评价两系统的优劣.
(本小题满分13分)已知函数 .
.
(1)若对于区间 内的任意
内的任意 ,总有
,总有 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(2)若函数 在区间
在区间 内有两个不同的零点
内有两个不同的零点 ,求:
,求:
①实数 的取值范围;②
的取值范围;② 的取值范围.
的取值范围.
(本小题满分13分)已知数列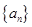 中,
中, ,其前
,其前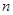 项和
项和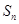 满足
满足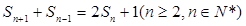 .
.
(1)求证:数列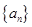 为等差数列,并求
为等差数列,并求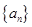 的通项公式;
的通项公式;
(2)设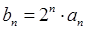 ,求数列
,求数列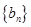 的前
的前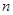 项和
项和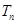 ;
;
(3)设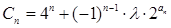 (
(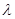 为非零整数,
为非零整数,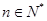 ),是否存在确定
),是否存在确定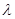 的值, 使得对任意
的值, 使得对任意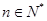 ,有
,有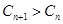 恒成立.若存在求出
恒成立.若存在求出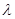 的值,若不存在说明理由。
的值,若不存在说明理由。
(本小题满分12分)已知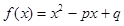 ,其中
,其中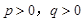 .
.
(1)当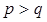 时,证明
时,证明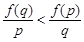 ;
;
(2)若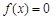 在区间
在区间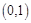 ,
,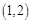 内各有一个根,求
内各有一个根,求 的取值范围.
的取值范围.
(本小题满分12分)在 中,角
中,角 所对的边为
所对的边为 ,且满足
,且满足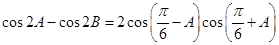
(1)求角 的值;
的值;
(2)若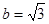 且
且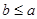 ,求
,求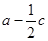 的取值范围
的取值范围
(本小题满分10分)记关于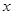 的不等式
的不等式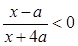 的解集为
的解集为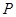 ,不等式
,不等式 的解集为
的解集为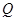 .
.
(1)若 ,求
,求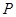 ;
;
(2)若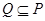 ,求
,求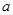 的取值范围.
的取值范围.