（本题8分）某中学开展演讲比赛活动，九(1)、九(2)班根据初赛成绩各选出5名选手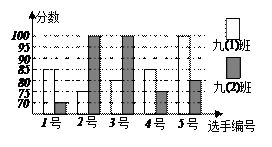
参加复赛，两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.
（1） 根据左图填写
下表
| |
平均分(分) |
中位数(分) |
众数(分) |
| 九(1)班 |
85 |
|
85 |
| 九(2)班 |
85 |
80 |
|
（2）结合两班复赛成绩的平均数和中位数，分析哪
个班级的复赛成绩较好？
（3）如果在每班参加复赛的选手中分别选出2人参
加决赛，你认为哪个班的实力更强一些，说明理由.
如图，抛物线
与
轴交于点A(－1，0)、B(3，0)，与
轴交于点C(0，3)．
(1)求抛物线的解析式及顶点D的坐标；
(2)若P为线段BD上的一个动点，点P的横坐标为m，试用含m的代数式表示点P的纵坐标；
(3)过点P作PM⊥x轴于点M，求四边形PMAC的面积的最大值和此时点P的坐标；
(4)若点F是第一象限抛物线上的一个动点，过点F作FQ∥AC交x轴于点Q．当点F的坐标为时，四边形FQAC是平行四边形；当点F的坐标为时，四边形FQAC是等腰梯形(直接写出结果，不写求解过程)．
如图，AB是⊙O的直径，直线EF切⊙O于点C，AD⊥EF于点D．
（1）求证：AC平分∠BAD；
（2）若⊙O的半径为2，∠ACD＝30°，求图中阴影部分的面积．（结果保留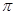
）
已知：
ABCD的两边AB、AD的长是关于
的方程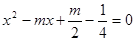
的两个实数根．
（1）当
为何值时，ABCD是菱形？求出这时菱形的边长；
（2）若AB=2，那么ABCD的周长是多少？
如图，抛物线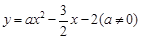
的图象与x轴交于A、B两点，与y轴交于C点，已知点B坐标为（4，0）．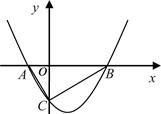
（1）求抛物线的解析式；
（2）判断△ABC的形状，说出△ABC外接圆的圆心位置，并求出圆心的坐标．
如图，四边形ABCD是矩形，对角线AC、BD相交于点O，BE∥AC交DC的延长线于点E．
（1）求证：BD＝BE；
（2）若ÐDBC＝30°，CD＝4，求四边形ABED的面积．