如图,抛物线 与
与 轴交于点A(-1,0)、B(3,0),与
轴交于点A(-1,0)、B(3,0),与 轴交于点C(0,3).
轴交于点C(0,3).
(1)求抛物线的解析式及顶点D的坐标;
(2)若P为线段BD上的一个动点,点P的横坐标为m,试用含m的代数式表示点P的纵坐标;
(3)过点P作PM⊥x轴于点M,求四边形PMAC的面积的最大值和此时点P的坐标;
(4)若点F是第一象限抛物线上的一个动点,过点F作FQ∥AC交x轴于点Q.当点F的坐标为 时,四边形FQAC是平行四边形;当点F的坐标为 时,四边形FQAC是等腰梯形(直接写出结果,不写求解过程).
画图说明题:
(1)借助手中的三角板,画∠AOB=90°
(2)在∠AOB的内部任画出一条射线OM
(3)画∠AOM的平分线OC,∠BOM的平分线OD
(4)用量角器量得∠COD=
试用说理的方法说明你所得结果的正确性.
某超市进了10箱橙子,每箱标准质量是50kg,到货后,超市又复称一遍,复称的结果如下:(超出标准质量为正,不足标准质量为负)
+0.5 +0.3 -0.9 +0.1 +0.4 -0.2 -0.7 +0.8 +0.3 +0.1
求超市共进了多少千克橙子?
(1)解方程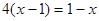 ;
;
(2)解方程 ;
;
(3)先化简,再求值:当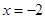 ,
,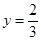 时,求
时,求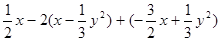 的值.
的值.
(1)-5×6×(- )×
)×
(2)(-24)×(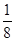 -
- +
+ )
)
(3)-12-[1 +(-12)÷6]2×(-
+(-12)÷6]2×(- )
)
我国是世界上严重缺水的国家之一,为了增强居民的节水意识,某自来水公司对居民用水采取以户为单位分段计费办法收费;即每月用水10吨以内(包括10吨)的用户,每吨水收费a元,每月用水超过10吨的部分,按每吨b元(b>a)收费,设一户居民月用水x(吨),应收水费y(元),y与x之间的函数关系如图所示.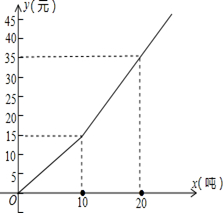
(1)分段写出y与x的函数关系式.
(2)某户居民上月用水8吨,应收水费多少元?
(3)已知居民甲上月比居民乙多用水4吨,两家一共交水费46元,求他们上月分别用水多少吨?