（本小题满分12分）
已知函数
（Ⅰ）若曲线y=
f(x)在点P（1，f(1)）处的切线与直线y=x+2垂直，求函数y=f(x)的单调区间；
（Ⅱ）若对于任意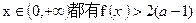
成立，试求a的取值范围；
（Ⅲ）记g(x)=f(x)+x-b(b∈R).当a=1时，函数g(x)在区间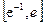
上有两个零点，求实数b的取值范围。
(本小题满分14分)已知
为坐标原点,点F、T、M、P分别满足
.
(1) 当t变化时,求点P的轨迹方程;
(2) 若
的顶点在点P的轨迹上,且点A的纵坐标
,的重心恰好为点F,
求直线BC的方程.
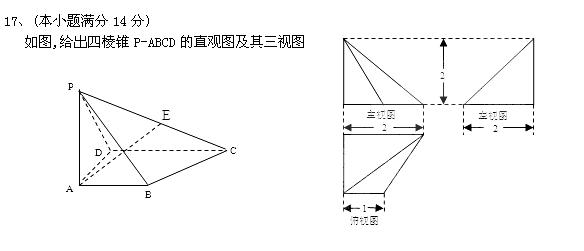
(1)、据此说明四棱锥P-ABCD具有的特征及已知条件;
(2)、由你给出的特征及条件证明:面PAD⊥面PCD
(3)、若PC中点为E,求直线AE与面PCD所成角的余弦值.
(本小题满分12分)高二级某次数学测试中,随机从该年级所有学生中抽取了100名同学的数学成绩(满分150分),经统计成绩在
的有6人,在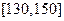
的有4人.在
,
各区间分布情况如右图所示的频率分布直方图,若直方图中,
和
对应小矩形高度相等,且
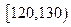对应小矩形高度又恰为对应小矩形高度的一半.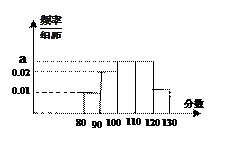
(1)确定图中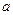
的值;
(2)设得分在110分以上(含110分)为优秀,则这次测试的优秀率是多少?
(3)某班共有学生50人,若以该次统计结果为依据,现随机从该班学生中抽出3人, 则至少抽到一名数学成绩优秀学生的概率是多少?
、(本小题满分12分)已知函数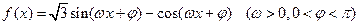
为偶函数,且其图象两相邻对称轴间的距离为
(1)求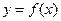
的解析式;
(2)若把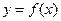图象按向量
平移,得到函数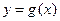
的图象,求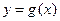
的单调增区间.
(本小题满分12分)已知△ABC中，角A,B,C的对边分别为a,b,c，且b=
c，sinA•cosC=3sinC•cosA.
(Ⅰ)若△ABC的面积S=
sinA，求c；
(Ⅱ)求
的值．