如图所示，在光滑的水平地面上有一块长木板，其左端固定一挡板，挡板和长木板的总质量为m1 =3kg，其右端放一质量为m2= 1kg的小滑块，长木板的右端到挡板的距离为L=lm，整个装置处于静止状态。现对小滑块施加一水平拉力，将它拉到长木板的正中央时立即撤去拉力，此过程中拉力做功W=20J。此后小滑块与挡板碰撞（碰撞过程无机械能损失，碰撞时间极短），最终小滑块恰好未从长木板上掉下来。在小滑
块与长木板发生相对运动的整个过程中，系统因摩擦产生热量Q=12J。求：
（1）小滑块最终的速度大小；
（2）碰撞结束时，小滑块与长木板的速度；
（3）在小滑块与长木板发生相对运动的整个过程中,小滑块运动的位移大小。
如图所示为质谱仪的原理图，A为粒子加速器，电压为U1；B为速度选择器，磁场与电场正交，磁感应强度为B1，板间距离为d；C为偏转分离器，磁感应强度为B2。今有一质量为m、电量为q的正离子经加速后，恰好通过速度选择器，进入分离器后做半径为R的匀速圆周运动，求：
⑴粒子的速度v；
⑵速度选择器的电压U2；
⑶粒子在B2磁场中做匀速圆周运动的半径R和运动时间t。
如图所示，PQ和MN为水平、平行放置的金属导轨，相距1m，导体棒ab跨放在导轨上，棒的质量m=0.2kg，棒的中点用细绳经滑轮与物体相连，物体质量M=0.3kg，棒与导轨间的动摩擦因数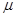
=0.5，匀强磁场的磁感应强度B=2T，方向竖直向下，为了使物体保持静止，应在棒中通入多大的电流？方向如何？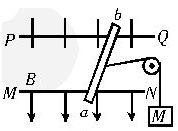
如图所示的电路中，电源的电动势为2V，内阻为0.5Ω， R0为2Ω，变阻器的阻值变化范围为0~10Ω，当S闭合后，求：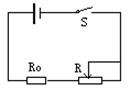
（1）变阻器阻值多大时，R0消耗的功率最大，其最大功率为多少？
（2）变阻器阻值多大时，变阻器消耗的功率最大，其最大功率为多少?
如图，一质量为1 kg的小球套在一根固定的直杆上，直杆与水平面夹角θ为30°，现小球在F=10N的沿杆向上的拉力作用下，从A点静止出发沿杆向上运动，已知杆与球间的动摩擦因数m为
。试求：
（1）小球运动的加速度a1；
（2）若F作用2s后撤去，小球上滑过程中距A点最大距离Sm；
（3）若从撤去力F开始计时，小球经多长时间将经过距A点上方为4.64m的B点。
如图甲所示，质量m=4kg的物体在水平面上向右做直线运动。过a点时给物体作用一个水平向左的恒力F并开始计时，选水平向右为速度的正方向，通过速度传感器测出物体的瞬时速度，所得v-t图象如图乙所示。（取重力加速度为10 m/s2）求：
(1)8s末物体离a点的距离
(2)力F的大小和物体与水平面间的动摩擦因数μ；