（本小题共12分）甲、乙两个射手进行射击训练，甲击中目标的概率为
，乙击中目标的概率为
，每人各射击两发子弹为一个“单位射击组”，若甲击中目标的次数比乙击中目标的次数多，则称此组为“单位进步组”。
（1）
求一个“单位射击组”为“单位进步组”的概率；
（2）记完成三个“单位射击组”后出现“单位进步组”的次数
，求的分布列与数学期望。
已知曲线C的极坐标方程为ρ2=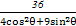
,以极点为原点,极轴所在直线为x轴建立平面直角坐标系.
(1)求曲线C的直角坐标方程及参数方程.
(2)若P(x,y)是曲线C上的一个动点,求x+2y的最小值,并求P点的坐标.
求直线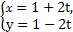
(t为参数)被圆
(α为参数)截得的弦长.
以直角坐标系的原点为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线l的极坐标方程为ρsin(θ-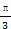
)=6,圆C的参数方程为
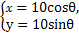(θ为参数),求直线l被圆C截得的弦长.
在曲线C1: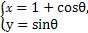
(θ为参数,0≤θ<2π)上求一点,使它到直线C2:
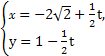(t为参数)的距离最小,并求出该点坐标和最小距离.
过点M(2,1)作曲线C: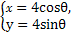
(θ为参数)的弦,使M为弦的中点,求此弦所在直线的方程.