(本小题满分10分)已知构成某系统的元件能正常工作的概率为p(0<p<1),且各个元件能否正常工作是相互独立的.今有2n(n大于1)个元件可按如图所示的两种联结方式分别构成两个系统甲、乙.
(1) 试分别求出系统甲、乙能正常工作的概率p1,p2;
试分别求出系统甲、乙能正常工作的概率p1,p2;
(2) 比较p1与p2的大小,并从概率意义上评价两系统的优劣.
已知函数 .
.
(Ⅰ)若 在
在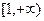 上是增函数,求实数a的取值范围.
上是增函数,求实数a的取值范围.
(Ⅱ)若 是
是 的极大值点,求
的极大值点,求 在
在 上的最大值;
上的最大值;
(Ⅲ)在(2)的条件下,是否存在实数b,使得函数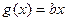 的图像与函数
的图像与函数 的图像恰有3个交点,若存在,求出b的取值范围,若不存在,说明理由.
的图像恰有3个交点,若存在,求出b的取值范围,若不存在,说明理由.
设函数
,已知
和
为
的极值点.
(Ⅰ)求
和
的值;
(Ⅱ)讨论函数
的单调性;
(Ⅲ)设
,比较
与
的大小.
已知函数 。
。
(1)若 ,证明:
,证明: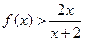 ;
;
(2)若不等式 对
对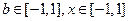 时恒成立,求实数
时恒成立,求实数 的取值范围。
的取值范围。
设函数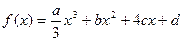 的图象关于原点对称,
的图象关于原点对称, 的图象在点
的图象在点 处的切线的斜率为
处的切线的斜率为 ,且当
,且当 时
时 有极值.
有极值.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的所有极值.
的所有极值.
已知函数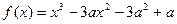

(1)求函数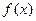 的单调区间;
的单调区间;
(2)曲线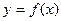 在点
在点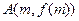 和
和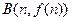
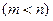 处的切线都与
处的切线都与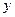 轴垂直,若曲线
轴垂直,若曲线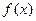 在区间
在区间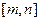 上与
上与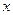 轴相交,求实数
轴相交,求实数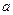 的取值范围;
的取值范围;