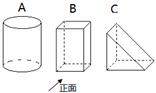
如图，A、B、C是三个几何体，箭头所指方向是它们的正面．设A、B、C三个几何体的主视图分别是A1、B1、C1；左视图分别是A2、B2、C2；俯视图分别是A3、B3、C3.
（1）请你分别写出A1、A2、A3、B1、B2、B3、C1、C2、C3所表示的图形的名称；
（2）小刚先将这9个视图分别画在大小、形状完全相同的9张卡片上，并将画有A1、A2、A3的三张卡片放在甲口袋中；画有B1、B2、B3的三张卡片放在乙口袋中；画有C1、C2、C3的三张卡片放在丙口袋中．然后由小强随机从这三个口袋中各取一张卡片．
①补全下面的树状图，并求小强随机抽取的三张卡片上图形名称都相同的概率．
②小刚和小强做游戏，游戏规则是：在小强随机抽取的三张卡片中，三张卡片上的图形名称都相同时，小刚获胜；三张卡片上的图形名称完全不同时，小强获胜．这个游戏对双方公平吗？为什么？
 |
|||
 |
|||
（本题5分）已知a、b为方程x2－2x－1＝0的两根，不解方程，求a2＋2b2－2a－4b＋3的值．
（本题8分）根据条件求下列抛物线的解析式：
(1)二次函数的图象经过(0，1)，(2，1)和(3，4)；
(2)抛物线的顶点坐标是（－2，1），且经过点（1，－2）．
解方程（本题8分）
(1)
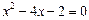(2)
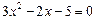
(本题满分10分)已知二次函数y＝x2＋bx－
3的图像经过点P(－2，5)．
（1）求b的值，并写出当0＜x≤3时y的取值范围；
（2）设点P1(m，y1)、P2(m＋1，y2)、P3(m＋2，y3)在这个二次函数的图像上．
①试比较y1和y2的大小；
②当m取不小于5的任意实数时，请你探索：y1、y2、y3能否作为一个三角形
三边的长，并说明理由．
(本题满分8分)通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角的正对(sad)．如图①在△ABC中，AB＝AC，顶角A的正对记作sad A，这时sad A
．容易知道一个角的大小与这个角的正对值也是相互
唯一确定的．根据上述角的正对定义，解下列问题：
（1）sad 60°＝．
（2）对于0°＜A＜180°，∠A的正对值sad A的取值范围是
（3）如图②，在Rt△ABC中，∠C＝90°，sin A
，试求sad A的值
|
A
 |
|||
 |