如图,已知∠MON=90º,等边△ABC的一个顶点A是射线OM上的一定点,顶点B与点O重合,顶点C在∠MON内部.
(1)当顶点B在射线ON上移动到B1时,连结AB1,请在∠MON内部作出以AB1为边的等边三角形AB1C1(保留作图痕迹,不写作法和证明);
(2)设AB1与OC交于点Q,AC的延长线与B1C1交于点D.求证:
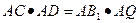
(3)连结CC1,试猜想∠ACC1为多少度?并证明你的猜想.
 |
如图,∠AOB是直角,射线OC从OA出发,以每秒8度的速度顺时针方向转动;射线OD从OB出发,以每秒2度的速度逆时针方向转动.当OC与OA成一直线时停止转动.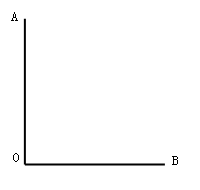
(1)______秒时,OC与OD重合.
(2)当OC与OD的夹角是30度时,求转动的时间是多少秒?
(3)若OB平分∠COD,求转动的时间是多少秒?并画出此时的OC与OD,写出图中∠AOD的余角.
已知:如图,B、C是线段AD上两点,且AB︰BC︰CD=2︰4︰3,M是AD的中点,CD=9cm,求线段MC的长.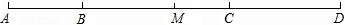
先化简,再求值: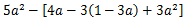 ,其中
,其中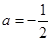 .
.
如图,将两块直角三角板的直角顶点C叠放在一起.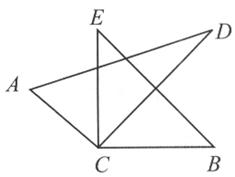
(1)若∠DCB=35°,求∠ACB的度数;
(2)若∠ACB=140°,求∠DCE的度数.
某公路检修队乘车从A地出发,在南北走向的公路上检修道路,规定向南走为正,向北走为负,从出发到收工时所行驶的路程记录如下(单位:千米):+3,-9,+4,+6,-10,+5,-3,+14.
(1)问收工时,检修队在A地哪边,距A地多远?
(2)问从出发到收工时,汽车共行驶多少千米?
(3)在汽车行驶过程中,若每行驶l千米耗油0.15升.公路检修队检查到第四处的加油站时,刚好油用完,加油时发现比上次加油时油价下跌了0.2元/升.检修队从A地出发到回到A地,共用油费64.98元.问此次加油的油价是每升多少元?