一手机经销商计划购进某品牌的A型、B型、C型三款手机共60部，每款手机至少要购进8部，且恰好用完购机款61000元．设购进A型手机x部，B型手机y部．三款手机的进价和预售价如下表：
| 手机型号 |
A型 |
B型 |
C型 |
| 进 价（单位：元/部） |
900 |
1200 |
1100 |
| 预售价（单位：元/部） |
1200 |
1600 |
1300 |
（1）用含x，y的式子表示购进C型手机的部数；
（2）求出y与x之间的函数关系式；
（3）假设所购进手机全部售出，综合考虑各种因素，该手机经销商在购销这批手机过程中需另外支出各种费用共1500元．
①求出预估利润P（元）与x（部）的函数关系式；（注：预估利润P＝预售总额-购机款-各种费用）
②求出预估利润的最大值，并写出此时购进三款手机各多少部．
某铁路桥长1000m，现有一列火车从桥上通过，测得该火车从开始上桥到完全过桥共用了1min，整列火车完全在桥上的时间共40s．求火车的速度和长度．
小明在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况（收入取整数，单位：元），并绘制了如下的频数分布表和频数分布直方图.
根据以上提供的信息，解答下列问题：
（1）补全频数分布表.
| 分组 |
频数 |
百分比 |
600≤ ＜800 |
2 |
5％ |
| 800≤＜1000 |
6 |
15％ |
| 1000≤＜1200 |
45％ |
|
| 9 |
22.5％ |
|
| 1600≤＜1800 |
2 |
|
| 合计 |
40 |
100％ |
（2）补全频数分布直方图.
（3）请你估计该居民小区家庭属于中等收入（大于1000不足1600元）的大约有多少户？
已知，如图，CD⊥AB于D，EF⊥AB于F，∠1=∠2，请问DG∥BC吗？如果平行，请说明理由。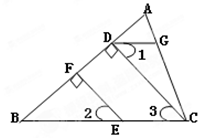
按要求画图（不写画法，保留作图痕迹）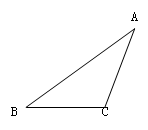
（1）画△ABC的高AD；
（2）画△ABC的角平分线BE
（3）画△ABC的中线CF
化简：