一个袋中有若干个大小相同的黑球、白球和红球。已知从袋中任意摸出1个球,得到黑球的概率是 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是 。
。
(Ⅰ)若袋中共有10个球,
(i)求白球的个数;
(ii)从袋中任意摸出3个球,记得到白球的个数为 ,求随机变量
,求随机变量 的数学期望
的数学期望 。
。
(Ⅱ)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于 。并指出袋中哪种颜色的球个数最少。
。并指出袋中哪种颜色的球个数最少。
已知各项都不相等的等差数列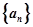 的前
的前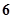 项和为
项和为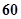 ,且
,且 为
为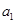 和
和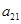 的等比中项.
的等比中项.
(I)求数列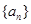 的通项公式;
的通项公式;
(II) 若数列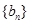 满足
满足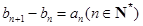 ,且
,且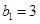 ,求数列
,求数列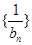 的前
的前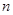 项和
项和 .
.
已知数列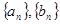 满足:
满足: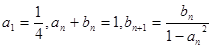
1)求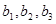 的值; 2)求证数列
的值; 2)求证数列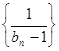 是等差数列,并求数列
是等差数列,并求数列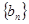 的通项公式;
的通项公式;
3)设 若
若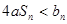 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
某企业投资1千万元于一个高科技项目,每年可获利25%.由于企业间竞争激烈,每年底需要从利润中取出资金 万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.设经过
万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.设经过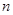 年后该项目的资金为
年后该项目的资金为 万元.
万元.
1)写出数列 的前三项
的前三项 ,并猜想写出通项
,并猜想写出通项 .
.
2)求经过多少年后,该项目的资金可以达到或超过 千万元.
千万元.
设 满足约束条件:
满足约束条件: 的可行域为
的可行域为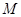
1)在所给的坐标系中画出可行域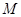 (用阴影表示,并注明边界的交点或直线);
(用阴影表示,并注明边界的交点或直线);
2)求 的最大值与
的最大值与 的最小值;
的最小值;
3)若存在正实数 ,使函数
,使函数 的图象经过区域
的图象经过区域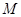 中的点,
中的点,
求这时 的取值范围.
的取值范围.
已知正项等差数列 的前
的前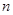 项和为
项和为 ,若
,若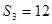 ,且
,且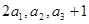 成等比数列.
成等比数列.
1)求 的通项公式
的通项公式 和
和 ; 2)记
; 2)记 的前
的前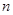 项和
项和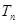 ,求
,求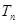 .
.