如图所示, xoy平面内的正方形区域abcd,边长为L,oa=od=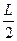 ,在该区域内有与y轴平行的匀强电场和垂直于平面的匀强磁场,一个带电粒子(不计重力)从原点沿+x轴进入场区,恰好沿+x轴直线射出。若撤去电场只保留磁场,其他条件不变,该粒子从cd边上距d点
,在该区域内有与y轴平行的匀强电场和垂直于平面的匀强磁场,一个带电粒子(不计重力)从原点沿+x轴进入场区,恰好沿+x轴直线射出。若撤去电场只保留磁场,其他条件不变,该粒子从cd边上距d点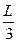 处射出,若撤去磁场,只保留电场,其他条件不变,该粒子从哪条边上何处射出?
处射出,若撤去磁场,只保留电场,其他条件不变,该粒子从哪条边上何处射出?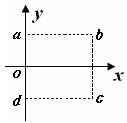
如图所示,U形管两细管粗细均匀长度相等,左端封闭,右端开口,水平部分长20cm。有两段8cm长水银柱等高,各封住长为30cm的空气柱A和长为40cm的空气柱B,两气体温度均为27oC,大气压强恒定。现使A、B温度缓慢升高,最终都达到57 oC。问:
(1)空气柱A的最终长度。
(2)右管内水银柱移动的距离。
(1)下列说法正确的是(本小题6分。在给出的四个选项中,可能只有一项符合题目要求,也可能有多项符合题目要求。全部选对的得6分,选对但不全的得3分,有选错的得0分)
| A.α粒子散射实验揭示了原子核有复杂结构 |
| B.用质子流工作的显微镜比用相同速度的电子流工作的显微镜分辨率高 |
| C.光电效应揭示了光具有粒子性 |
| D.原子核结合能越大,则原子核越稳定 |
(2)太阳内部四个质子聚变成一个粒子,同时发射两个正电子和两个没有静止质量的中微子。若太阳辐射能量的总功率P,质子、氦核、正电子的质量分别为mp、mHe、me,真空中光速为c,求t时间内参与核反应的质子数。
(1)在以下说法中,正确的是(本小题6分。在给出的四个选项中,可能只有一项符合题目要求,也可能有多项符合题目要求。全部选对的得6分,选对但不全的得3分,有选错的得0分)
| A.电磁波谱包括无线电波、红外线、可见光、紫外线、X射线、γ射线 |
| B.牛顿环是薄膜干涉的结果,当用频率更高的单色光照射时,同级牛顿环半径将会变大 |
| C.机械波是介质传递波源质点以及振动能量的一种方式 |
| D.麦克耳孙-莫雷实验结果表明:不论光源与观察者做怎样的相对运动,光速都是一样的 |
(2)如图所示,半圆玻璃砖的半径R=10cm,折射率为n=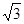 ,直径AB与屏幕垂直并接触于A点.激光a以入射角i=30°射向半圆玻璃砖的圆心O,结果在水平屏幕MN上出现两个光斑.求两个光斑之间的距离L.
,直径AB与屏幕垂直并接触于A点.激光a以入射角i=30°射向半圆玻璃砖的圆心O,结果在水平屏幕MN上出现两个光斑.求两个光斑之间的距离L.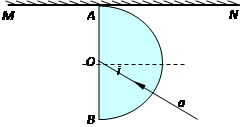
1.分子动理论很好地解释了物质的宏观热力学性质,据此可判断下列说法中正确的
是(本小题6分。在给出的四个选项中,可能只有一项符合题目要求,也可能有多项符合题目要求。全部选对的得6分,选对但不全的得3分,有选错的得0分)
| A.显微镜下观察到墨水中小炭粒在不停地做无规则运动,这反映了液体分子运动的无规则性 |
| B.随着分子间距离的增大,分子间的相互作用力一定先减小后增大 |
| C.随着分子间距离的增大,分子势能可能先减小后增大 |
| D.在真空、高温条件下,可以利用分子扩散向半导体材料掺入其他元素 |
2.一定质量的理想气体由状态A经状态B变为状态C,其中A→B过程为等压变化,B→C过程为等容变化.已知VA=0.3 m3,TA=TC=300K,TB=400 K.
(1) 求气体在状态B时的体积.
(2) 说明B→C过程压强变化的微观原因.
(3)设A→B过程气体吸收热量为Q1,B→C过程气体放出热量为Q2,比较Q1、Q2的大小并说明原因.
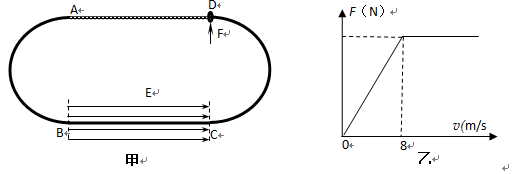
如图甲所示, A、B、C、D为固定于竖直平面内的闭合绝缘轨道,AB段、CD段均为半径R=1.6m的半圆,BC、AD段水平,AD=BC=8m。B、C之间的区域存在水平向右的有界匀强电场,场强E=5×105V/m,其余区域没有电场。质量为m=4×10-3kg、带电量q=+1×10-8C的小环套在轨道上。小环与轨道AD段的动摩擦因数为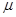 =0.125,与轨道其余部分的摩擦忽略不计。现使小环在D点获得沿轨道向左的初速度v0=4m/s,且在沿轨道DA段运动过程中始终受到方向竖直向上、大小随速度变化的力F(变化关系如图乙所示)作用,小环第一次进入半圆轨道AB时在A点对半圆轨道刚好无压力。不计小环大小,g取10m/s2。求:
=0.125,与轨道其余部分的摩擦忽略不计。现使小环在D点获得沿轨道向左的初速度v0=4m/s,且在沿轨道DA段运动过程中始终受到方向竖直向上、大小随速度变化的力F(变化关系如图乙所示)作用,小环第一次进入半圆轨道AB时在A点对半圆轨道刚好无压力。不计小环大小,g取10m/s2。求:
(1)小环第一次运动到A时的速度大小;
(2)小环第一次回到D点时速度大小;
(3)若小环经过多次循环运动能达到稳定运动状态,则到达D点时的速度至少多大?