本小题满分12分)(注意:在试题卷上作答无效)
在进行一项掷骰子放球的游戏中规定:若掷出1点或2点,则在甲盒中放一球;否则,在乙盒中放一球。现在前后一共掷了4次骰子,设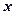 、
、 分别表示甲、乙盒子中球的个数。
分别表示甲、乙盒子中球的个数。
(Ⅰ)求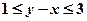 的概率;
的概率;
(Ⅱ)若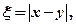 求随机变量
求随机变量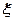 的分布列和数学期望。
的分布列和数学期望。
如图,在四棱锥 中,四边形
中,四边形 为平行四边形,
为平行四边形, 为
为 上一点,且
上一点,且 .
.
(Ⅰ)求证: ;
;
(Ⅱ)若点 为线段
为线段 的中点,求证:.
的中点,求证:.

时维壬辰,序属仲春,值春耕播种时机,某中学生物研究性学习小组对春季昼夜温差大小与水稻发芽率之间的关系进行研究,记录了实验室4月10日至4月14日的每天昼夜温差与每天每50颗稻籽浸泡后的发芽数,得到如下资料:
| 日期 |
4月10日 |
4月11日 |
4月12日 |
4月13日 |
4月14日 |
| 温差x(oC) |
10 |
12 |
13 |
14 |
11 |
| 发芽数y(颗) |
11 |
13 |
14 |
16 |
12 |
(Ⅰ)从4月10日至4月14日中任选2天,记发芽的种子数分别为m,n,求事件“m,n均小于14”的概率;
(Ⅱ)根据表中的数据可知发芽数y(颗)与温差x(oC)呈线性相关,请求出发芽数y关于温差x的线性回归方程 .
.
(参考公式:回归直线方程式 ,其中
,其中 )
)
在 中,角
中,角 所对的边分别为
所对的边分别为 ,且
,且 成等差数列.
成等差数列.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,试求
,试求 周长
周长 的范围.
的范围.
在数列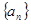 中,已知
中,已知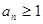 ,
,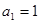 ,且
,且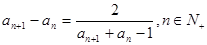 .
.
(1)记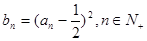 ,求证:数列
,求证:数列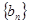 是等差数列;
是等差数列;
(2)求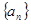 的通项公式;
的通项公式;
(3)对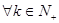 , 是否总
, 是否总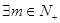 使得
使得 ?若存在,求出
?若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
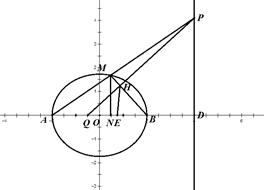
已知椭圆 :
: 与双曲线
与双曲线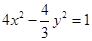 有相同的焦点,且椭圆
有相同的焦点,且椭圆 的离心率
的离心率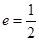 ,又
,又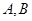 为椭圆的左右顶点,
为椭圆的左右顶点, 为椭圆上任一点(异于
为椭圆上任一点(异于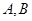 ).
).
(1)求椭圆的方程;
(2)若直线 交直线
交直线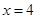 于点
于点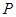 ,过
,过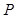 作直线
作直线 的垂线交
的垂线交 轴于点
轴于点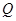 ,求
,求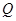 的坐标;
的坐标;
(3)求点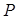 在直线
在直线 上射影
上射影 的轨迹方程.
的轨迹方程.