已知椭圆的一个顶点为A(0,-1),焦点在x轴上,若右焦点到
直线 的距离为3。
的距离为3。
(1)求椭圆的方程;
(2)设直线 与椭圆相交于不同的两点M,N,当|AM|=|AN|时,求m的
与椭圆相交于不同的两点M,N,当|AM|=|AN|时,求m的
取值范围.
某工厂对一批产品进行了抽样检测.下图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是6。
(1)样本中净重大于或等于98克并且小于104克的产品的个数是多少?
(2)估计该批产品净重的平均值。
(3)若从净重小于100克的样品中抽取两个产品,求两个样品净重都在[98,100)的概率。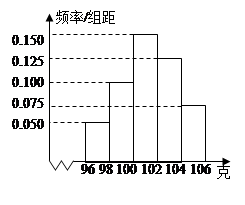
已知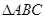 的三个角
的三个角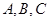 所对的边分别为
所对的边分别为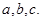 且满足
且满足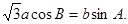
(1) 求角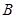 的大小
的大小
(2) 求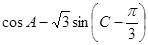 的取值范围.
的取值范围.
已知双曲线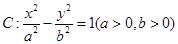 的一个焦点与抛物线
的一个焦点与抛物线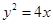 的焦点重合,且双曲线的离心率为
的焦点重合,且双曲线的离心率为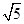 .
.
(1)求双曲线的方程;
(2)若有两个半径相同的圆 ,它们的圆心都在
,它们的圆心都在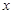 轴上方且分别在双曲线
轴上方且分别在双曲线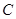 的两条渐近线上,过双曲线右焦点且斜率为
的两条渐近线上,过双曲线右焦点且斜率为 的直线
的直线 与圆
与圆 都相切,求两圆圆心连线的斜率的范围。
都相切,求两圆圆心连线的斜率的范围。
设数列 的前项n和为
的前项n和为 ,若对于任意的正整数n都有
,若对于任意的正整数n都有 .
.
(1)设 ,求证:数列
,求证:数列 是等比数列,并求出
是等比数列,并求出 的通项公式。
的通项公式。
(2)求数列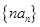 的前n项和
的前n项和 .
.
已知椭圆 的中心在原点,它的左右两个焦点分别为
的中心在原点,它的左右两个焦点分别为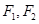 ,过右焦点
,过右焦点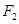 且与
且与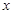 轴垂直的直线
轴垂直的直线 与椭圆
与椭圆 相交,其中一个交点为
相交,其中一个交点为
(1) 求椭圆 的方程。
的方程。
(2)设椭圆 的一个顶点为
的一个顶点为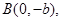 直线
直线 交椭圆
交椭圆 于另一点
于另一点 ,求
,求 的面积.
的面积.