某水产养殖场拟造一个无盖的长方体水产养殖网箱，为了避免混养，箱中要安装一些筛网，其平面图如下，如果网箱四周网衣（图中实线部分）建造单价为每米56元，筛网（图中虚线部分）的建造单价为每米48元，网箱底面面积为160平方米，建造单价为每平方米50元，网衣及筛网的厚度忽略不计.
（1）把建造网箱的总造价y（元）表示为网箱的长x（米）的函数，并求出最低造价；
（2）若要求网箱的长不超过15米，宽不超过12米，则当网箱的长和宽各为多少米时，可使总造价最低？（结果精确到0.01米）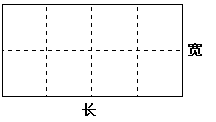
已知点
为圆
上的动点，且不在
轴上，
轴，垂足为
，线段
中点
的轨迹为曲线
，过定点
任作一条与
轴不垂直的直线
，它与曲线交于
、
两点。
（I）求曲线的方程；
（II）试证明：在轴上存在定点
，使得
总能被轴平分
设函数
．
（I）求
的单调区间；
（II）当0<a<2时，求函数
在区间
上的最小值．
为了解高中一年级学生身高情况，某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查，测得身高频数分布表如下表1、表2．
表1：男生身高频数分布表
| 身高（cm） |
[160，165） |
[165，170） |
[170，175） |
[175，180） |
[180，185） |
[185，190） |
| 频数 |
2 |
5 |
14 |
13 |
4 |
2 |
表2：女生身高频数分布表
| 身高（cm） |
[150，155） |
[155，160） |
[160，165） |
[165，170） |
[170，175） |
[175，180） |
| 频数 |
1 |
7 |
12 |
6 |
3 |
1 |
（I）求该校男生的人数并完成下面频率分布直方图；
（II）估计该校学生身高在
的概率；
（III）从样本中身高在180
190cm之间的男生中任选2人，求至少有1人身高在185190cm之间的概率。
在边长为
的正方形ABCD中，E、F分别为BC、CD的中点，M、N分别为AB、CF的中点，现沿AE、AF、EF折叠，使B、C、D三点重合，构成一个三棱锥．
（I）判别MN与平面AEF的位置关系，并给出证明；
（II）求多面体E-AFMN的体积．
已知函数
（
），相邻两条对称轴之间的距离等于
．
（Ⅰ）求
的值；
（Ⅱ）当
时，求函数
的最大值和最小值及相应的x值．