在平面几何中,已知“正三角形内一点到三边距离之和是一个定值”,类比到空间写出你认为合适的结论: .
某初级中学领导采用系统抽样方法,从该校预备年级全体800名学生中抽50名学生做牙齿健康检查。现将800名学生从1到800进行编号,求得间隔数为16。在1~16中随机抽取一个数,如果抽到的是7,则从49 ~ 64这16个数中应取的是
已知下列命题:
①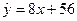 意味着
意味着 每增加一个单位,
每增加一个单位, 平均增加8个单位
平均增加8个单位
②投掷一颗骰子实验,有掷出的点数为奇数和掷出的点数为偶数两个基本事件
③互斥事件不一定是对立事件,但对立事件一定是互斥事件
④在适宜的条件下种下一颗种子,观察它是否发芽,这个实验为古典概型
其中正确的命题有__________________.
已知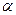 是第二象限的角,
是第二象限的角, ,则
,则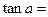 .
.
 的弧度数为________________.
的弧度数为________________.
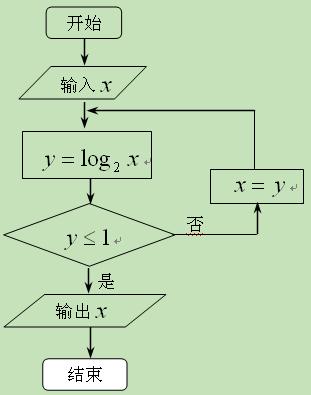
执行右图所示的程序框图,若输入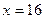 ,则输出
,则输出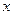 的值为.
的值为.