已知函数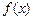
＝
＋
，a≠0且a≠1．
（1）试就实数a的不同取值，写出该函数的单调增区间；
（2）已知当x＞0时，函数在(0，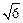
)上单调递减，在(，
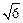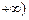上单调递增，求a的值并写出函数的解析式；
（3）记（2）中的函数图象为曲线C，试问是否存在经过原点的直线l，使得l为曲线C的对称轴？若存在，求出直线l的方程；若不存在，请说明理由．
某中学从参加高一年级上期期末考试的学生中抽出60名学生，将其成绩（均为整数）分成六段
，
…
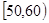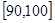后画出如下部分频率分布直方图.观察图形的信息，回答下列问题：
（Ⅰ）估计这次考试的及格率（60分及以上为及格）；
(Ⅱ) 从成绩是70分以上（包括70分）的学生中选一人，求选到第一名学生的概率（第一名学生只一人）.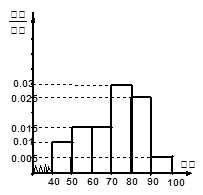 
已知函数
（1）
时，求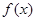
的单调区间；
（2）设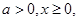
若
恒成立，求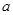
的取值范围.
如图，已知圆C：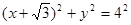
，定点A（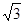
，0），M为圆C上一动点，点N在AM上，点P在 CM上，且满足
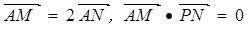，点P的轨迹为曲线E，
（1）求曲线E 的方程；
（2）当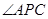
为钝角，求点P的横坐标的取值范围。
（1）已知x , y>0,且x+y>2，试证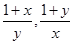
中至少有一个小于2。
（2）已知|a|<1，|b|<1，求证：
>1
已知函数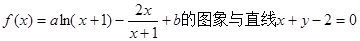
相切于点（0，c）。 求：（1）实数a的值；（2）函数
的单调区间和极小值。