（本小题满分12分）
已知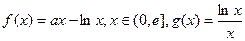
，其中
是自然常数，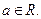
（1）讨论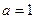
时,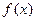 
的单调性、极值；
（2）求证：在（1）的条件下，
；
（3）是否存在实数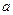
，使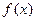的最小值是3，若存在，求出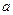的值；若不存在，说明理由.
在
中，内角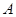
、
、
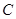对边分别是
、
、
，已知
，
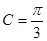（1）(1)求的面积
的最大值；
（2）若
,求的面积．
解关于x的不等式
（
）
已知:如右图,在等腰梯形ABCD中,AD∥BC,AB＝DC,过点D作AC的平行线DE,交BA的延长线于点E．求证：(1)△ABC≌△DCB (2)DE·DC＝AE·BD．
已知抛物线
和点
，过点P的直线
与抛物线交与
两点，设点P刚好为弦
的中点。
（1）求直线的方程
（2）若过线段上任一
（不含端点）作倾斜角为
的直线交抛物线于
，类比圆中的相交弦定理，给出你的猜想，若成立，给出证明；若不成立，请说明理由。
（3）过P作斜率分别为
的直线
，
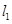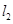交抛物线于，
交抛物线于
，是否存在使得（2）中的猜想成立，若存在，给出
满足的条件。若不存在，请说明理由。
抛物线
（p>0）的准线与x轴交于M点，过点M作直线l交抛物线于A、B两点.
（1）若线段AB的垂直平分线交x轴于N（x0，0），比较x0与3p大小；
（2）若直线l的斜率依次为p，p2，p3，…，线段AB的垂直平分线与x轴的交点依次为N1，N2，N3，…，求
+
+…+
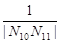的值.