已知椭圆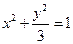 (0<b<1)的左焦点为F,左、右顶点分别为A,C,上顶点为B,过F、B、C作⊙P,其中圆心P的坐标为(m,n)。
(0<b<1)的左焦点为F,左、右顶点分别为A,C,上顶点为B,过F、B、C作⊙P,其中圆心P的坐标为(m,n)。
(1)当m+n>0时,求椭圆离心率的范围;
(2)直线AB与⊙P能否相切?证明你的结论。
符合下列三个条件之一,某名牌大学就可录取:
①获国家高中数学联赛一等奖(保送录取,联赛一等奖从省高中数学竞赛优胜者中考试选拔);
②自主招生考试通过并且高考分数达到一本分数线(只有省高中数学竞赛优胜者才具备自主招生考试资格);
③高考分数达到该大学录取分数线(该大学录取分数线高于一本分数线).
某高中一名高二数学尖子生准备报考该大学,他计划:若获国家高中数学联赛一等奖,则保送录取;若未被保送录取,则再按条件②、条件③的顺序依次参加考试.
已知这名同学获省高中数学竞赛优胜奖的概率是0.9,通过联赛一等奖选拔考试的概率是0.5,通过自主招生考试的概率是0.8,高考分数达到一本分数线的概率是0.6,高考分数达到该大学录取分数线的概率是0.3.
(I)求这名同学参加考试次数 的分布列及数学期望;
的分布列及数学期望;
(II)求这名同学被该大学录取的概率.
对于给定数列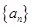 ,如果存在实常数
,如果存在实常数 ,使得
,使得 对于任意
对于任意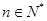 都成立,我们称数列
都成立,我们称数列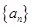 是 “
是 “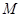 类数列”.
类数列”.
(Ⅰ)已知数列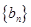 是 “
是 “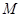 类数列”且
类数列”且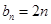 ,求它对应的实常数
,求它对应的实常数 的值;
的值;
(Ⅱ)若数列 满足
满足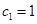 ,
, ,求数列
,求数列 的通项公式.并判断
的通项公式.并判断 是否为“
是否为“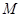 类数列”,说明理由.
类数列”,说明理由.
选修4-5:不等式选讲
设 .
.
(I)求不等式 的解集S:
的解集S:
(II)若关于x不等式 有解,求参数t的取值范围.
有解,求参数t的取值范围.
选修4-4:坐标系与参数方程
以直角坐标系的原点O为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线l的参数方程为 (t为参数,
(t为参数, ),曲线C的极坐标方程为
),曲线C的极坐标方程为 ,
,
(I )求曲线C的直角坐标方程:
(II)设直线l与曲线C相交于A、B两点,当a变化时,求|AB|的最小值.
选修4-1:几何证明选讲
如图,AB是圆O的直径,以B为圆心的圆B与圆O的一个交点为P.过点A作直线交圆O于点Q,交圆B于点M、N.
(I )求证:QM=QN;
(II)设圆O的半径为2,圆B的半径为1,当AM= 时,求MN的长.
时,求MN的长.