对于给定数列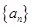 ,如果存在实常数
,如果存在实常数 ,使得
,使得 对于任意
对于任意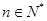 都成立,我们称数列
都成立,我们称数列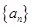 是 “
是 “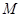 类数列”.
类数列”.
(Ⅰ)已知数列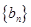 是 “
是 “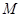 类数列”且
类数列”且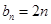 ,求它对应的实常数
,求它对应的实常数 的值;
的值;
(Ⅱ)若数列 满足
满足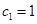 ,
, ,求数列
,求数列 的通项公式.并判断
的通项公式.并判断 是否为“
是否为“ 类数列”,说明理由.
类数列”,说明理由.
已知四棱锥 底面ABCD是矩形,PA⊥平面ABCD, AD=2,AB=1,E.F
底面ABCD是矩形,PA⊥平面ABCD, AD=2,AB=1,E.F
分别是线段AB.BC的中点,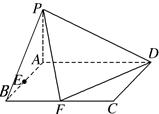
(1)证明:PF⊥FD;
(2)在PA上找一点G,使得EG∥平面PFD;.
(3)若 与平面
与平面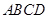 所成的角为
所成的角为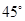 ,求二面角
,求二面角 的余弦值.
的余弦值.
已知△ 的三个内角
的三个内角 、
、 、
、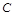 所对的边分别为
所对的边分别为 、
、 、
、 .
.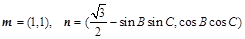 ,且
,且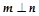 .(1)求
.(1)求 的大小;(2)若
的大小;(2)若 .求
.求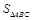 .
.
已知数列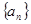 满足
满足 ,
,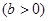 ,
,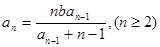 .
.
(1)求数列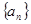 的通项公式;
的通项公式;
(2)证明:对于一切正整数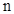 ,有
,有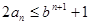 .
.
已知函数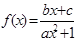 (
( )是奇函数,
)是奇函数, 有最大值
有最大值
且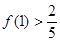 .
.
(1)求函数 的解析式;
的解析式;
(2)是否存在直线 与
与 的图象交于P、Q两点,并且使得
的图象交于P、Q两点,并且使得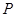 、
、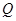 两点关于点
两点关于点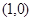 对称,若存在,求出直线
对称,若存在,求出直线 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
在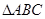 中,角
中,角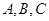 所对的边分别为
所对的边分别为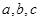 ,向量
,向量 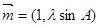 ,
, .已知
.已知  .
.
(1)若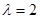 ,求角A的大小;
,求角A的大小;
(2)若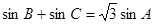 ,求
,求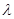 的取值范围.
的取值范围.