设 为非零实数, .
(I) 写出
并判断
是否为等比数列.若是,给出证明;若不是,说明理由;
(II)设
,求数列
的前
项和
.
(本小题满分10分)
设函数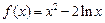 .
.
(I)若当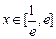 时,不等式
时,不等式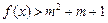 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(II)若关于x的方程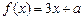 在区间[
在区间[ 1,3]上恰好有两个相异的实根,求实数
1,3]上恰好有两个相异的实根,求实数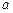 的取值范围.
的取值范围.
四、附加题:本大题共2小题,每小题10分,共20分。
(20)(本小题满分10分)
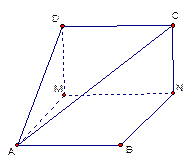
已知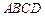 是边长为1的正方形,
是边长为1的正方形,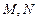 分别为
分别为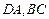 上的点,且
上的点,且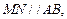 沿
沿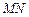 将正方形折成直二面角
将正方形折成直二面角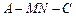 .
.
(I)求证:平面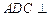 平面
平面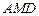 ;
;
(II)设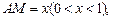 点
点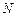 与平面
与平面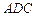 间的距离为
间的距离为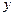 ,试用
,试用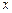 表示
表示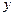 .
.
(本小题满分10分)
已知函数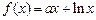
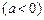 .
.
(I)求 的单调区间;
的单调区间;
(II)设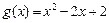 ,若对任意
,若对任意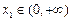 ,均存在
,均存在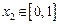 ,使得
,使得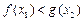 ,求
,求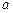 的取值范围.
的取值范围.
(本小题满分10分)
如图,四面体ABCD中,O是BD的中点,ΔABD和ΔBCD均为等边三角形,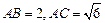 .
.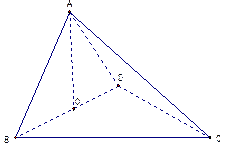
(I)求证: 平面BCD;
平面BCD;
(II)求二面角A-BC- D的正切值.
(本小题满 分10分)
分10分)
如图,在正四棱柱ABCD-A1 B1C1D1中,AA1 =
B1C1D1中,AA1 =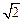 ,AB = 1,E是DD1的中点.
,AB = 1,E是DD1的中点.
(I)求直线B1D和平面A1ADD1所成角的大小;
(II)求证:B1D⊥AE.