在平面直角坐标系 上,给定抛物线 .实数 满足 , 是方程 的两根,记
(1)过点 作 的切线教 轴于点 .证明:对线段 上任一点 有 ;
(2)设 是定点,其中 满足 , .过 作 的两条切线 ,切点分别为 , 与y轴分别交与 .线段 上异于两端点的点集记为 .证明: ;
(3)设 .当点 取遍 时,求 的最小值 (记为 )和最大值(记为 ).
(本小题满分14分)
已知一非零向量列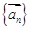 满足:
满足: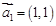 ,
,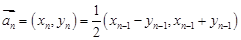
 .
.
(1)证明: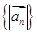 是等比数列;
是等比数列;
(2)设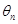 是
是 的夹角
的夹角 ,
,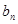 =
=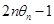 ,
, ,求
,求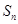 ;
;
(3)设
 ,问数列
,问数列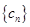 中是否存在最小项?若存在,求出最小值;若不存在,请说明理由.
中是否存在最小项?若存在,求出最小值;若不存在,请说明理由.
已知函数 ,
,
(1)求 的最小值;
的最小值;
(2)若对所有 都有
都有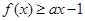 ,求实数
,求实数 的取值范围.
的取值范围.
(本题满分12分)
某商店经销一种洗衣粉,年销售总量为6000包,每包进价为2.8元,销售价为3.4元,全年分若干次进货,每次进货均为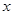 包,已知每次进货的运输劳务费为62.5元,全部洗衣粉一年的保管费为1.5
包,已知每次进货的运输劳务费为62.5元,全部洗衣粉一年的保管费为1.5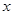 元.
元.
(1)将该商店经销洗衣粉一年的利润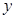 (元)表示为每次进货量
(元)表示为每次进货量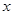 (包)的函数;
(包)的函数;
(2)为使利润最大,每次应进货多少包?
(本小题满分14分)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD
所在的平面和圆O所在的平面互相垂直,且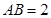 ,
, .
.
(1)求证: 平面
平面 ;
;
(2)设FC的中点为M,求证: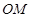 ∥平面
∥平面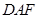 ;
;
(3)求三棱锥F-CBE的体积.
(本小题满分14分)
已知向量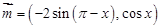 ,
, ,函数
,函数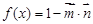 .
.
(1)求函数 的解析式;
的解析式;
(2)当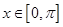 时,求
时,求 的单调递增区间;
的单调递增区间;
(3)说明 的图象可以由
的图象可以由 的图象经过怎样的变换而得到.
的图象经过怎样的变换而得到.