如图所示,沿波的传播方向上有间距为1m的13个质点a.b.c.d.e.f.g.h.I.j.k.l.m,它们均静止在各自的平衡位置。一列横波以1m/s的速度水平向右传播,在t=0时刻到达质点a,且a开始由平衡位置向上振动,在t=1s时刻,质点a第一次达到最高点,求:
①这列波的波长和周期;
②从a开始振动,经过多长时间d点第一次向下达到最大位移;
③在上图中画出d点第一次向下达到最大位移时的波形图像。
2011年7月11日23时41分,我国在西昌卫星发射中心用长征三号丙运载火箭,成功将“天链一号02星”送入太空。“天链一号02星”是我国第二颗地球同步轨道数据中继卫星,它将与2008年发射的“天链一号01星”组网运行,为我国神舟飞船以及未来空间实验室、空间站建设提供数据中继和测控服务,并将应用于我国将于2011年下半年实施的首次空间交会对接任务。若用m表示“天链一号02星”的质量,h 表示它离地面的高度,R0表示地球的半径,go表示地球表面处的重力加速度,T表示地球自转周期,万有引力常量为G。求:
(1)“天链一号02星”受到地球对它的万有引力的大小(用含有m、go、R0、h的字母表示);
(2)地球赤道表面的物体随地球自转的线速度与“天链一号02星”环绕速度的比值;
(3)利用上述数据计算出地球的质量M(用含有G、T、R0、h的字母表示)?
如图所示,在直角坐标系XOY平面内,在Y>0处有与X轴成60°角的匀强电场,场强大小E=103v/m,在Y<0处有垂直于纸面向外的匀强磁场,磁感应强度B= T。现从t=0时刻在坐标为(0,10
T。现从t=0时刻在坐标为(0,10 cm)的P点由静止释放一比荷为104C/kg的带正电的微粒A,不计微粒的重力。求:
cm)的P点由静止释放一比荷为104C/kg的带正电的微粒A,不计微粒的重力。求:
(1)微粒进入磁场后在磁场中运动的半径;
(2)第二次穿过X轴的时刻;
(3)在释放微粒A后又在电场中由静止释放另一个与A完全相同的微粒B,若要使微粒A在第二次穿过X轴到第三次穿过X轴的时间内与微粒B相遇,求微粒B释放的时刻和释放的位置。
质量为m=1kg的小物块轻轻放在水平匀速运动的传送带上的P点,随传送带运动到A点后水平抛出,小物块恰好无碰撞的沿圆弧切线从B点进入竖直光滑的圆孤轨道下滑。B、C为圆弧的两端点,其连线水平。已知圆弧半径R=1.0m圆弧对应圆心角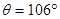 ,轨道最低点为O,A点距水平面的高度h=0.8m,小物块离开C点后恰能无碰撞的沿固定斜面向上运动,0.8s后经过D点,物块与斜面间的动摩擦因数为
,轨道最低点为O,A点距水平面的高度h=0.8m,小物块离开C点后恰能无碰撞的沿固定斜面向上运动,0.8s后经过D点,物块与斜面间的动摩擦因数为 =
= (g=10m/s2,sin37°=0.6,cos37°=0.8)试求:
(g=10m/s2,sin37°=0.6,cos37°=0.8)试求:
(1)小物块离开A点时的水平初速度v1。
(2)小物块经过O点时对轨道的压力。
(3)假设小物块与传送带间的动摩擦因数为 0.3,传送带的速度为5m/s,则PA间的距离是多少?
0.3,传送带的速度为5m/s,则PA间的距离是多少?
(4)斜面上CD间的距离。
如图,质量 的物体静止于水平地面的A处,A、B间距L=20m。用大小为30N,沿水平方向的外力拉此物体,经
的物体静止于水平地面的A处,A、B间距L=20m。用大小为30N,沿水平方向的外力拉此物体,经 拉至B处。(已知
拉至B处。(已知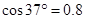 ,
,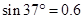 。取
。取 )
)
(1)求物体与地面间的动摩擦因数μ;
(2)用大小为30N,与水平方向成37°的力斜向上拉此物体,使物体从A处由静止开始运动并能到达B处,求该力作用的最短时间t。
在一次消防逃生演练中,队员从倾斜直滑道AB的顶端A由静止滑下,经B点后水平滑出,最后落在水平地面的保护垫上(不计保护垫厚度的影响)。已知A、B离水平地面的高度分别为H=6.2m、h=3.2m,A、B两点间的水平距离为L=4.0m,队员与滑道间的动摩擦因数μ=0.3,g取10m/s2。求: 
(1)队员到达B点的速度大小;
(2)队员落地点到B点的水平距离;