(本小题满分14分)已知函数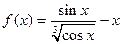
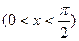 .
.
(1)求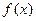 的导数
的导数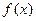 ;
;
(2)求证:不等式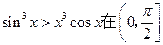 上恒成立;
上恒成立;
(3)求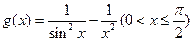 的最大值.
的最大值.
(本题12分)已知实数a,b,c,d满足a+b+c+d=3,a2+2b2+3c2+6d2=5,
求证:(Ⅰ)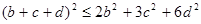 ;
;
(Ⅱ)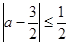 .
.
(本题12分)如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=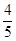 |PD|.
|PD|.
(Ⅰ)当P在圆上运动时,求点M的轨迹C的方程;
(Ⅱ)求过点(3,0)且斜率为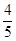 的直线被曲线C所截线段的长度.
的直线被曲线C所截线段的长度.
(本题12分)如图,在长方体ABCD-A1B1C1D1中,E, F分别是棱BC,CC1上的点,CF="AB=2CE," AB:AD:AA1=1:2:4.
(Ⅰ)求异面直线EF与A1D所成角的余弦值;
(Ⅱ)证明AF⊥平面A1ED;
(Ⅲ)求二面角A1-ED-F的正弦值。
(本题12分)已知集合
(Ⅰ)在区间(-4,4)上任取一个实数x,求“x∈A∩B”的概率;
(Ⅱ)设(a,b)为有序实数对,其中a是从集合A中任取的一个整数,b是从集合B中任取的一个整数,求“b-a∈A∪B”的概率.
(本题10分)某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30min抽取一包产品,称其重量,分别记录抽查数据如下:
甲:102, 101, 99, 98, 103, 98, 99;
乙:110, 115, 90, 85, 75, 115, 110。
(Ⅰ)这种抽样方法是哪一种?
(Ⅱ)将这两组数据用茎叶图表示出来;
(Ⅲ)将两组数据比较:说明哪个车间的产品较稳定。