已知函数
.
(I)讨论
的单调性;
(II)设
,证明:当
时,
;
(III)若函数 的图像与x轴交于
两点,线段
中点的横坐标为
,
的图像与x轴交于
两点,线段
中点的横坐标为
,
证明:
已知椭圆的长轴长为2a,焦点是F1(-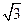 ,0)、F2(
,0)、F2(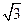 ,0),点F1到直线x=-
,0),点F1到直线x=-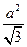 的距离为
的距离为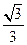 ,过点F2且倾斜角为锐角的直线l与椭圆交于A、B两点,使得|F2B|=3|F2A|.
,过点F2且倾斜角为锐角的直线l与椭圆交于A、B两点,使得|F2B|=3|F2A|.
(1)求椭圆的方程;
(2)求直线l的方程.
已知椭圆x2+(m+3)y2=m(m>0)的离心率e=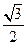 ,求m的值及椭圆的长轴和短轴的长及顶点坐标.
,求m的值及椭圆的长轴和短轴的长及顶点坐标.
自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在直线的方程。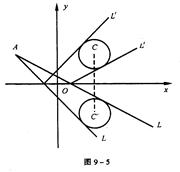
已知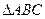 的顶点
的顶点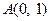 ,
,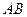 边上的中线
边上的中线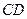 所在的直线方程为
所在的直线方程为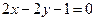 ,
,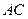 边上的高
边上的高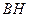 所在直线的方程为
所在直线的方程为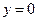 .
.
(1)求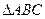 的顶点
的顶点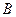 、
、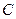 的坐标;
的坐标;
(2)若圆 经过不同的三点
经过不同的三点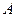 、
、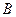 、
、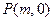 ,且斜率为
,且斜率为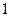 的直线与圆
的直线与圆 相切于点
相切于点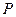 ,求圆
,求圆 的方程.
的方程.
设椭圆的中心在原点,焦点在x轴上,离心率e=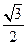 .已知点P
.已知点P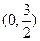 到这个椭圆上的点的最远距离为
到这个椭圆上的点的最远距离为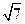 ,求这个椭圆的方程.
,求这个椭圆的方程.