已知点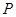 是⊙
是⊙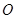 :
: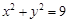 上的任意一点,过
上的任意一点,过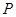 作
作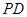 垂直
垂直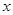 轴于
轴于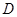 ,动点
,动点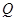 满足
满足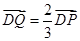 。
。
(1)求动点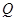 的轨迹方程;
的轨迹方程;
(2)已知点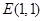 ,在动点
,在动点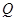 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点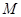 、
、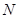 ,使
,使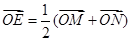 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线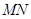 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
在数列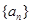 中,
中,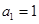 ,
,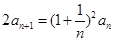
(1)求数列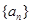 的通项公式;
的通项公式;
(2)令 ,求数列
,求数列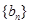 的前
的前 项和
项和
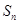 .
.
在海岛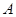 上有一座海拔
上有一座海拔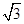 千米的山,山顶设有一个观察站
千米的山,山顶设有一个观察站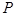 ,上午
,上午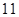 时,测得一轮船在海岛北偏东
时,测得一轮船在海岛北偏东 ,俯角(与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,当目标视线在水平视线的下方时称为俯角)为
,俯角(与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,当目标视线在水平视线的下方时称为俯角)为 的
的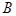 处。到
处。到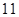 时
时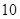 分又测得该轮船在岛西偏北
分又测得该轮船在岛西偏北 ,俯角为
,俯角为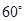 的
的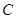 处。
处。
(1)该轮船的航行速度是每小时多少千米?
(2)又经过一段时间后,轮船到达海岛正西方向的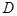 处,此时轮船距岛有多远?
处,此时轮船距岛有多远?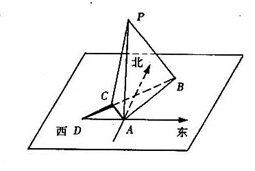
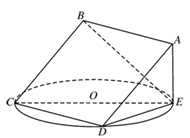
如图,四棱锥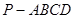 的底面为直角梯形,
的底面为直角梯形,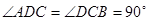 ,
, ,
, ,
,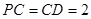 ,
,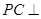 平面
平面
(1)在线段 上是否存在一点
上是否存在一点 ,使平面
,使平面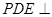 平面
平面 ,如果存在,说明E点位置;如果不存在,说明理由.
,如果存在,说明E点位置;如果不存在,说明理由.
(2)求二面角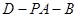 的余弦值.
的余弦值.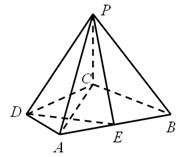
在 中,内角
中,内角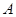 、
、 、
、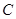 对边分别是
对边分别是 、
、 、
、 ,已知
,已知 ,
,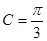 (1)(1)求
(1)(1)求 的面积
的面积 的最大值;
的最大值;
(2)若 ,求
,求 的面积.
的面积.
解关于x的不等式 (
( )
)