围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为2m的进出口,如图所示已知旧墙的维修 费用为45元/m,新墙的造价为180元/m,设利用的旧墙长
费用为45元/m,新墙的造价为180元/m,设利用的旧墙长 度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元)
度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元)
⑴将y表示为x的函数;
⑵写出f(x)的单调区间(不必证明)
⑶根据⑵,试确定x, 使修建此矩形场地围墙的总费用最小,并求出最小总费用。
使修建此矩形场地围墙的总费用最小,并求出最小总费用。
如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.
(1)求实数b的值;
(2)求以点A为圆心,且与抛物线C的准线相切的圆的方程.
(本小题满分13分)如图,四棱锥,底面矩形 中,
中, ,
,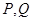 分别为线段
分别为线段 、
、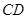 的中点,
的中点,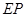 ⊥平面
⊥平面 .
.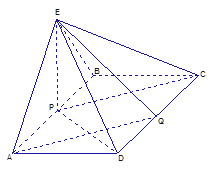
(1)求证: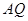 ∥平面
∥平面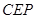 ;
;
(2)求证:平面 ⊥平面
⊥平面 ;
;
(本小题满分13分)已知集合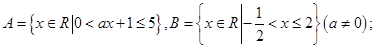
(1)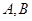 能否相等?若能,求出实数
能否相等?若能,求出实数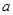 的值,若不能,试说明理由?
的值,若不能,试说明理由?
(2)若命题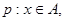 命题
命题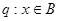 且
且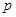 是
是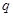 的充分不必要条件,求实数
的充分不必要条件,求实数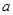 的取值范围.
的取值范围.
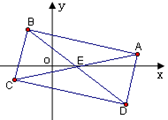
(本小题满分13分)如图,已知长方形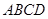 的两条对角线的交点为
的两条对角线的交点为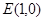 ,且
,且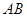 与
与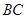 所在的直线方程分别为
所在的直线方程分别为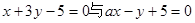 .
.
(1)求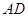 所在的直线方程;
所在的直线方程;
(2)求出长方形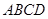 的外接圆的方程.
的外接圆的方程.
已知椭圆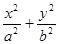 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=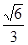 ,过点A(0,-b)和B(a,0)的直线与坐标原点距离为
,过点A(0,-b)和B(a,0)的直线与坐标原点距离为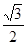 .
.
(1)求椭圆的方程;
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆相交于C、D两点,试判断是否存在k值,使以CD为直径的圆过定点E?若存在求出这个k值,若不存在说明理由.