已知a、b是两个互不相等的正实数,比较A=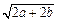 与B=
与B=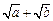 的大小。
的大小。
(本小题8分)已知数列 的前
的前 项和
项和 .
.
(1)计算 ,
, ,
, ,
, ;
;
(2)猜想 的表达式,并用数学归纳法证明你的结论.
的表达式,并用数学归纳法证明你的结论.
(本小题满分8分) 已知函数 .
.
(1)求函数f(x)的单调区间;
(2)已知a、b∈R,a>b>e, (其中e是自然对数的底数), 求证:ba >ab.
(本小题满分8分)已知抛物线C:y=-x2+4x-3 .
(1)求抛物线C在点A(0,-3)和点B(3,0)处的切线的交点坐标;
(2)求抛物线C与它在点A和点B处的切线所围成的图形的面积.
(本小题满分14分)在 的展开式中,把
的展开式中,把 叫做三项式系数.
叫做三项式系数.
(Ⅰ)当 时,写出三项式系数
时,写出三项式系数 的值;
的值;
(Ⅱ)二项式 的展开式中,系数可用杨辉三角形数阵表示,如图:
的展开式中,系数可用杨辉三角形数阵表示,如图:
当 时,类似杨辉三角形数阵表,请列出三项式的
时,类似杨辉三角形数阵表,请列出三项式的 次系数列的数阵表;
次系数列的数阵表;
(Ⅲ)求 的值(可用组合数作答).
的值(可用组合数作答).
(本小题满分12分)4月10日,2015《中国汉字听写大会》全国巡回赛浙江赛区在杭州宣布正式启动,并拉开第三届“汉听大会”全国海选的帷幕。某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示.
(Ⅰ)求频率分布直方图中 的值,试估计全市学生参加汉字听写考试的平均成绩;
的值,试估计全市学生参加汉字听写考试的平均成绩;
(Ⅱ)如果从参加本次考试的同学中随机选取1名同学,求这名同学考试成绩在80分以上(含80分)的概率;
(Ⅲ)如果从参加本次考试的同学中随机选取3名同学,这3名同学中考试成绩在80分以上(含80分)的人数记为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
(注:频率可以视为相应的概率)