（为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法调查该地区老人情况:男老年人需要提供帮助40人，不需要提供帮助160人；女老年人需要提供帮助30人，不需要提供帮助270人.
(Ⅰ)根据调查数据制作2×2列联表;
(Ⅱ)能否有99℅的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
| 参考数据 |
当 ≤2.706时，无充分证据判定变量A，B有关，可以认为两变量无关； |
| 当＞2.706时，有90%把握判定变量A，B有关； |
|
| 当＞3.841时，有95%把握判定变量A，B有关； |
|
当＞6. 635时，有99%把握判定变量A，B有关。 |
（请考生在题22，23，24中任选一题作答，如果多做，则按所做的第一题计分。）
（本小题满分10分）已知圆锥曲线
是参数）和定点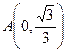
，F1、F2是圆锥曲线的左、右焦点。
（1）求经过点F2且垂直地于直线AF1的直线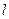
的参数方程；
（2）以坐标原点为极点，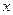
轴的正半轴为极轴建立极坐标系，求直线AF2的极坐标方程。
（请考生在题22，23，24中任选一题作答，如果多做，则按所做的第一题计分。）
（本小题满分10分）如图5，⊙O1和⊙O2公切线AD和BC相交于点D，A、B、C为切点，直线DO1与⊙O1与E、G两点，直线DO2交⊙O2与F、H两点。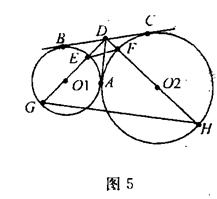
（1）求证：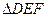
～
；
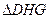（2）若⊙O1和⊙O2的半径之比为9：16，求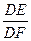
的值。
（本小题满分12分）已知函数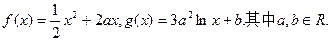
（1）设两曲线
与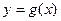
有公共点，且在公共点处的切线相同，若
，试建立
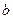关于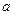
的函数关系式；
（2）在（1）的条件下求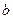的最大值；
（3
）若
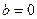时，函数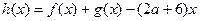
在（0，4）上为单调函数，求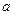的取值范围。
（本小题满分12分）已知定点C（-1，0）及椭圆
，过点C的动直线与椭圆相交于A，B两点。
（1）若线段AB中点的横坐标是
，求直线AB的方程；
（2）在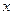
轴上是否存在点M，使
为常数？若存在，求出点M的坐标；若不存在，请说明理由。
（本小题满分12分）如图4，四棱锥P—ABCD中，底面ABCD是直角梯形，AB//CD，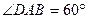
，AB=AD=2CD，侧面
底面ABCD，且
为等腰直角三角形，
，M为AP的中点。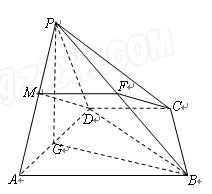
（1）求证：
（2）求证：DM//平面PCB。