如图: 是
是 的两条切线,
的两条切线, 是切点,
是切点, 是
是 上两点,如果
上两点,如果 ,试求
,试求 的度数.
的度数.
已知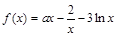 ,其中
,其中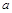 为常数.
为常数.
(Ⅰ)当函数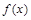 的图象在点
的图象在点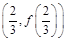 处的切线的斜率为1时,求函数
处的切线的斜率为1时,求函数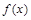 在
在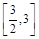 上的最小值;
上的最小值;
(Ⅱ)若函数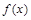 在
在 上既有极大值又有极小值,求实数
上既有极大值又有极小值,求实数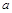 的取值范围;
的取值范围;
(Ⅲ)在(Ⅰ)的条件下,过点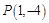 作函数
作函数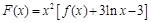 图象的切线,试问这样的切线有几条?并求这些切线的方程.
图象的切线,试问这样的切线有几条?并求这些切线的方程.
设函数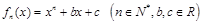
(Ⅰ)设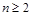 ,
,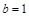 ,
,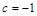 ,证明:
,证明: 在区间
在区间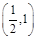 内存在唯一的零点;
内存在唯一的零点;
(Ⅱ)设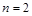 ,若对任意
,若对任意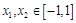 ,均有
,均有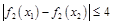 ,求
,求 的取值范围.
的取值范围.
设函数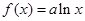 ,
, .
.
(1)记 为
为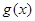 的导函数,若不等式
的导函数,若不等式 在
在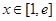 上有解,求实数
上有解,求实数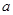 的取值范围;
的取值范围;
(2)若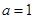 ,对任意的
,对任意的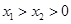 ,不等式
,不等式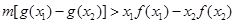 恒成立,求m(m∈Z,m
恒成立,求m(m∈Z,m 1)的值.
1)的值.
在 中,内角
中,内角 所对的边分别是
所对的边分别是 ,已知
,已知 .
.
(Ⅰ)若 ,
, ,求
,求 的外接圆的面积;
的外接圆的面积;
(Ⅱ)若 ,
, ,求
,求 的面积.
的面积.
命题p:实数 满足
满足 (其中
(其中 ),命题q:实数
),命题q:实数 满足
满足
(1)若 ,且
,且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(2)若 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.