设函数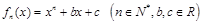
(Ⅰ)设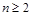 ,
,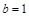 ,
,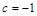 ,证明:
,证明: 在区间
在区间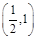 内存在唯一的零点;
内存在唯一的零点;
(Ⅱ)设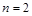 ,若对任意
,若对任意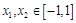 ,均有
,均有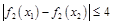 ,求
,求 的取值范围.
的取值范围.
设数列{an}的前n项和为Sn,且Sn=4an﹣p,其中p是不为零的常数.
(1)证明:数列{an}是等比数列;
(2)当p=3时,若数列{bn}满足bn+1=bn+an(n∈N*),b1=2,求数列{bn}的通项公式.
已知函数f(x)=sin(2x﹣ )+2cos2x﹣1(x∈R)
)+2cos2x﹣1(x∈R)
(1)求f(x)的单调递增区间;
(2)在△ABC中,三内角A,B,C的对边分别为b、a、c,若f(A)= ,且
,且 •
• =9,b,a,c成等差数列,求角A及a的值.
=9,b,a,c成等差数列,求角A及a的值.
已知等比数列{an}的各项均为正数,且2a1,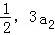 成等差数列,a2,
成等差数列,a2, ,a6成等比数列.
,a6成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=log3 ,记Sn=
,记Sn= ,求Sn.
,求Sn.
(1)已知在△ABC中,sinA+cosA= ,求tanA的值.
,求tanA的值.
(2)已知π<a<2π,cos(α﹣7π)=﹣ ,求sin(3π+α)•tan(α﹣
,求sin(3π+α)•tan(α﹣ π)的值.
π)的值.
已知椭圆C: +
+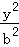 =1(a>b>0)过点(1,
=1(a>b>0)过点(1, ),且长轴长等于4.
),且长轴长等于4.
(Ⅰ)求椭圆C的方程;
(Ⅱ)F1,F2是椭圆C的两个焦点,⊙O是以F1,F2为直径的圆,直线l:y=kx+m与⊙O相切,并与椭圆C交于不同的两点A,B,若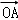 •
•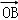 =﹣
=﹣ ,求k的值.
,求k的值.