已知椭圆C: +
+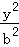 =1(a>b>0)过点(1,
=1(a>b>0)过点(1, ),且长轴长等于4.
),且长轴长等于4.
(Ⅰ)求椭圆C的方程;
(Ⅱ)F1,F2是椭圆C的两个焦点,⊙O是以F1,F2为直径的圆,直线l:y=kx+m与⊙O相切,并与椭圆C交于不同的两点A,B,若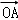 •
•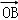 =﹣
=﹣ ,求k的值.
,求k的值.
(本题满分12分)在数列{an}中,已知a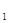 =-20,a
=-20,a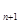 =a
=a +4(n∈
+4(n∈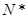 ).
).
(1)求数列{an}的通项公式和前n项和An;
(2)若 (n∈
(n∈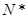 ),求数列{bn}的前n项Sn.
),求数列{bn}的前n项Sn.
(本题14分)已知抛物线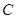 的顶点为坐标原点
的顶点为坐标原点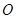 ,焦点
,焦点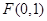 ,(1)求抛物线
,(1)求抛物线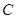 的方程;
的方程;
(2) 过点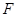 作直线交抛物线
作直线交抛物线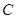 于
于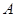 、
、 两点,若直线
两点,若直线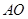 与
与 分别交直线
分别交直线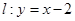 于
于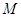 、
、 两点,当
两点,当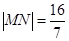 时,求直线
时,求直线 的方程。
的方程。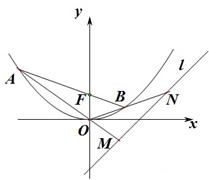
(本题14分)
已知函数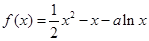 ,
,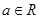 .
.
(1)若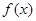 在区间
在区间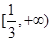 上单调递增,求
上单调递增,求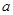 的取值范围;
的取值范围;
(2)试讨论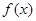 的单调区间.
的单调区间.
(本题14分)
已知数列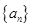 的前
的前 项和为
项和为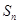 ,且
,且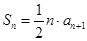 ,其中
,其中
(1)求数列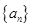 的通项公式;
的通项公式;
(2)若 ,数列
,数列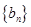 的前
的前 项和为
项和为 ,求证:
,求证: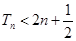
(本题14分)
已知平行四边形 ,
,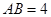 ,
, ,
,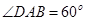 ,
, 为
为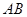 的中点,把三角形
的中点,把三角形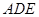 沿
沿 折起至
折起至 位置,使得
位置,使得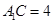 ,
,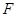 是线段
是线段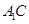 的中点.
的中点.
(1)求证: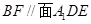 ;
;
(2)求证:面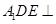 面
面 ;
;
(3)求四棱锥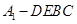 的体积.
的体积.